
И снова всем здравствуйте! Лонгмоб «Теория Эволюции» перевалил уже за середину, а это значит, что у нас очередные вести с полей, и очередная интересная тема.
На данный момент в закромах моба 3 прозы на конкурсе, 3 стиха на конкурсе, а так же 5 стихов и 8 рассказов в внеконкурсе.
Всего, значит, 13 внеконкурсов!
Так же, нам всё равно очень нужны Ваши ответы, Ваше внимание и Ваши работы.
Приходите на «Теорию Эволюции»!
writercenter.ru/library/poeziya/sbornik-rasskazov/longmob-teoriya-evolyucii/

Кое-что остаётся в моей памяти. К счастью, стать по поднятой теме сохранилась и в Википедии. А зачит, сегодня я расскажу Вам пожалуй о самой необычной игре, подходящей к лонгмобу.
Удивительная игра «Жизнь»
По большей части материал взят отсюда ru.wikipedia.org/wiki/%D0%96%D0%B8%D0%B7%D0%BD%D1%8C_(%D0%B8%D0%B3%D1%80%D0%B0) и из статью за 08. 89-г приложения к журналу Юный Техник «Для умелых рук».
Итак, когда-то к этому замечательному журналу было очень классное приложение. Там описывались всевозможные самоделки, а так же головоломки и игры. В одном из таких приложений (16 страничек на газетной бумаге), я прочитал про игру английского математика Джона Конвея на основе модели Джона фон Неймана.
Фон Нейман пытался создать гипотетическую машину, способную к воспроизводству. Конвей сформулировал ряд простых правил на бесконечном клеточном поле игры.
Представьте себе поле для крестиков-ноликов. У игровой зоны возможны границы, или же верхний край соприкасается с нижним, а левый с правым, — в таком случае мы получаем развёртку поверхности тора на плоскости. У каждой клетки на этом поле может быть восемь соседей.
Правила таковы:
1). Клетка, у которой есть два или три соседа, переходит в новое поколение. Если соседей меньше двух или больше трёх клетка умирает («от одиночества» или «от перенаселённости».
2). В клетке, рядом с которой ровно три клетки, зарождается жизнь.
Игрок задаёт расположение клеток на поле. А дальше лишь только следит за развитием клеток в соответствии с данными правилами.
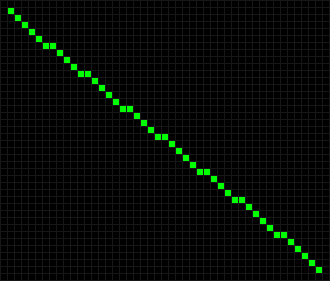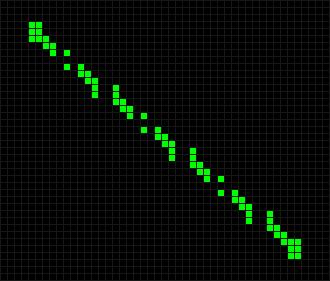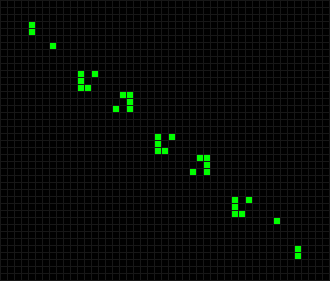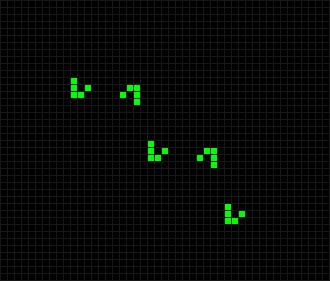
В результате исследований было обнаружено несколько классов объектов.
В первую очередь это устойчивые объекты.
Класс неизменных объектов
И несколько видов долгожителей, которые долгое время меняются, прежде чем стабилизироваться.
Периодические фигуры, повторяющиеся через определённое число повторений.
Двигающиеся фигуры, повторяющиеся с определённым смещением. Например число «90» из клеток, которое является планером.
Одной из самых известных фигур является планер, который был даже предложен в качестве символики хакеров.
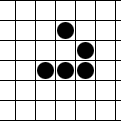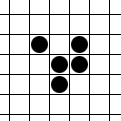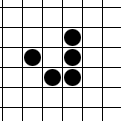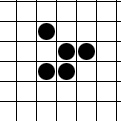
Клеточный автомат Планер.
На стоклеточном торе планер просто летает по кругу.

Ружья, — повторяющие фигуры, время от времени «выстреливающие» движущей частью.
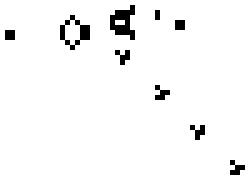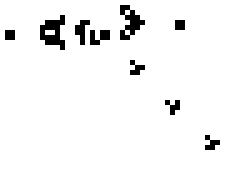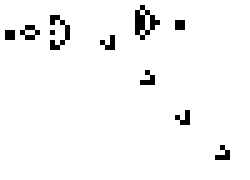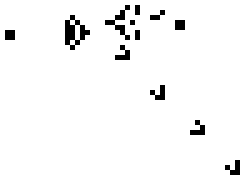
Ружьё Госпера стреляет планером
Паровозы оставляют за собой следы в виде устойчивых, или периодических фигур.
Пожиратели способны пережить столкновение с некоторыми из двигающихся фигур.
Сорняки копируют себя при столкновении с некоторыми другими фигурами.
Райским садом (садом Эдема) называется такое расположение клеток, у которого не может быть предыдущего поколения. Так понимаю, никакая расстановка по правилам не может его сгенерировать в будущем поколении, т.е. фигура из божественного вмешательства, без эволюции и без прошлого.
Практически для любой игры, состояние клеток в которой определяется несколькими соседями, можно доказать существование садов Эдема, но построить конкретную фигуру гораздо сложнее.

Достоверное изображение Райского Сада.
Конвей первоначально предположил, что никакая начальная комбинация не может привести к неограниченному размножению и предложил премию в 50 долларов тому, кто докажет или опровергнет эту гипотезу. Приз был получен группой из Массачусетского технологического института, придумавшей неподвижную повторяющуюся фигуру, которая периодически создавала движущиеся «планеры». Таким образом, количество живых клеток могло расти неограниченно. Затем были найдены движущиеся фигуры, оставляющие за собой «мусор» из других фигур.
Обнаружились многие связи закономерностей из игры «Жизнь» с другими науками. Иными словами, модель Конвея и Неймана можно использовать для описания разных процессов в других науках.
Кибернетика. Сама игра является удачной попыткой Конвея доказать существование простых самовоспроизводящихся систем.
Биология. Внешнее сходство с развитием популяций примитивных организмов впечатляет.
Физиология. Рождение и смерть клеток аналогичны процессу возникновения и исчезновения нейронных импульсов, которые и формируют процесс мышления. А также аналогичны созданию импульсов в нервной системе многоклеточных организмов.
Астрономия. Эволюции некоторых сложных колоний удивительным образом схематично повторяют этапы развития спиралевидных галактик.
Физика твёрдого тела. Теория автоматов вообще и игра «Жизнь» в частности используются для анализа «явлений переноса» — диффузии, вязкости и теплопроводности.
Квантовая физика. Поведение «жизненных» ячеек (рождение новых и взаимное уничтожение) во многом напоминают процессы, происходящие при столкновении элементарных частиц.
Наномеханика. Стационарные и пульсирующие колонии являются показательным примером простейших устройств, созданных на основе нанотехнологий.
Электротехника. Правила игры используются для моделирования самовосстанавливающихся электрических цепей.
Химия. Конфигурации, подобные строящимся в игре, возникают во время химических реакций на поверхности, в частности в опытах М. С. Шакаевой возникают движущиеся молекулярные конструкции аналогичные «жизненному» планеру. Также предпринимаются попытки объяснить периодические химические реакции с помощью многомерных клеточных автоматов. Самоорганизацией элементарных частиц также занимается супрамолекулярная химия.
Социология. Процессы доминации, вытеснения, поглощения, сосуществования, слияния и уничтожения популяций во многих аспектах схожи с явлениями, происходящими при взаимодействии больших, средних и малых социальных групп.
Философия. Приведённый список примеров снова наводит на мысль, что всё во Вселенной развивается по одним и тем же нескольким фундаментальным законам, пока ещё не познанным человеком.
Было доказано, что никакая фигура не может передвигаться по полю быстрее чем одна клетка по диагонали за генерацию. Эта скорость названа в теории Конвейна «скоростью света». Соответственно, максимальная скорость фигур по горизонтали и вертикали составляет половину от скорости света.

Надеюсь, что Вам понравилась эта статья. Предлагаю Вам вспомнить книги в фантастике, сильно «завязанные» на эволюцию и математику.







Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.
Если вы используете ВКонтакте, Facebook, Twitter, Google или Яндекс, то регистрация займет у вас несколько секунд, а никаких дополнительных логинов и паролей запоминать не потребуется.