Глава 4. Аналогии

Аналогия есть единственный возможный посредник

между видимым и невидимым, между конечным и бесконечным.

Элифас Леви. «Догма»

Одним из весьма эффективных способов познания неизведанного является, на мой взгляд, метод аналогий.

Имея возможность «отработать» новые теории или предположения на хорошо известных и действующих моделях, мы получаем шанс (набравшись определенной смелости) отметить много нового в Мироздании более высокого порядка.

Так получилось, что наиболее мне знакомым и хорошо изученным устройством для подобного проведения аналогий является цифровой компьютер. Именно на основе его архитектуры и принципов его функционирования я и буду вести анализ и сравнение.

Аналогия 1: Цифровой детерминизм

Будущее нельзя предвидеть, но можно изобрести.

Денис Габор

Принципы, положенные в работу цифровых компьютеров, делают их строго детерминированными устройствами.

Можно считать, что состояние изолированного компьютера полностью определяется информацией, записанной в его основную (оперативную) память и регистровую память процессора (Вообще говоря, его состояние может зависеть и от содержимого кэш-памяти микропроцессора, и от значений на интерфейсе входных устройств (клавиатура, модем, дисковод). Договоримся, однако, для простоты, что в данном случае содержимое кэш-памяти не оказывает подобного влияния (или же входит в определение «оперативная память»). Долговременную память (CD, DVD и т. п.) в этом случае мы рассматриваем как средство архивирования основной (оперативной) памяти. Действительно, процессор не в состоянии напрямую обратиться к определенной порции данных на жестком диске. Впрочем, если так удобнее, то вполне можно включить все эти устройства памяти также в определение «оперативная память» Связью же с «окружающим Миром», как и было сказано, рассматриваемый компьютер не обладает.)

Условимся так же, что основная программа обработки этих данных (будь то компьютерная игра, математические расчеты или что-то еще) хранится где-то в оперативной памяти отдельно от них[1]. Причем результаты работы этой программы не способны ее исказить. (Это ограничение равносильно положению о неизменности физических законов в нашей Вселенной. Действительно, принято считать, что и миллионы и миллиарды лет назад наш Мир развивался по тем же законам, что и сегодня.)

Тогда процессор и указанную программу можно будет условно представить в виде черного ящика, как это принято в кибернетике (Рисунок 18).

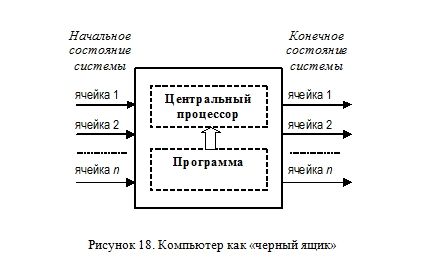
Входным параметром в этом случае будет являться вектор значений начального состояния компьютера, а выходом — состояние спустя некоторый промежуток времени (определенное число циклов работы процессора).

Цифровая сложность

Эйнштейн утверждал, что должны существовать

простые объяснения природных процессов,

так как Бог не действует из каприза или по произволу.

У программиста нет такого утешения:

сложность с которой он должен справиться,

лежит в самой природе системы.

F. Brooks. “No Silver Bullet”

Алгоритм, заложенный в программу может быть, вообще говоря, настолько сложным, что уже спустя несколько циклов работы процессора содержимое памяти изменится до неузнаваемости. Однако, несмотря на это, подобный переход является, как и было показано, полностью детерминированным.

Число всех возможных состояний ЭВМ хотя и огромно, но конечно. Если представить их в виде множества узлов, а направление перехода из одного состояние в другое (за один цикл работы процессора) в виде множества дуг, то получим ориентированный граф (Рисунок 19).

Отличительной особенностью этой схемы являются следующие ее свойства:

1. Дуги, соединяющие узлы, не изменяют свою ориентацию на протяжении всего времени работы компьютера. Другими словами, для заданного типа процессора конфигурация путей перехода из одного состояния в другое остается неизменной.

2. Существует лишь один вариант перехода из любого состояния в другое. То есть отсутствуют бифуркации (разветвления) дуг. Из одного узла может выходить только одна дуга. (Но в него могут вести несколько путей, как, например, для узла 6 на представленном рисунке.)

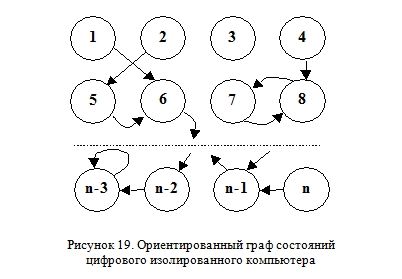
Именно благодаря этим свойствам поведение работы программы и является полностью детерминированным.

Можно представить себе ситуацию, когда путь перехода зацикливается («закольцовывается») на некотором множестве состояний (например, состояния 7 и 8) или даже на одном узле («тупиковое» состояние n-3). В этом случае изменение носит либо периодический характер, либо вообще прекращается. Можно, в принципе, найти и такие изолированные состояния, в которых система никогда не окажется (например, узел 3).

Представим себе, что рассмотренный вариант изолированного цифрового компьютера является моделью некоторого Мира. Видно, что подобный взгляд на Мироздание хорошо отражает позицию ученых материалистов-редукционистов. Свое начало подобное математическое истолкование Мироустройства идет, пожалуй, от сэра И. Ньютона с его основными законами динамики. Попытаемся провести некоторые аналогии между механистическим детерминизмом («классическая» механика) и детерминизмом «электронным» (e-механика).

E-механика

Последователь учений Ньютона французский физик и математик П. Лаплас на основе развитой им теории выдвинул возможность (пусть и теоретическую) существования некого крайне могущего существа — демона, способного по измеренным координатам и векторам скорости каждой точки пространства точно предсказать наперед их дальнейшее положение.

«Ум, — говорил он, — которому были бы известны для какого-либо данного момента все силы, одушевляющие природу, и относительное положение всех ее составных частей, если бы вдобавок он оказался достаточно обширным, чтобы подчинить эти данные анализу, объял бы в одной формуле движение величайших тел Вселенной, наравне с движением легчайших атомов: не осталось бы ничего, что было бы для него недостоверно, и будущее, так же как и прошедшее, предстало бы перед его взором».

Подобный наблюдатель Лапласа, способный окинуть своим взглядом всю Вселенную и узнать с абсолютной точностью положения и скорости всей ее составляющих, вошел в историю науки, как демон Лапласа[2].

Представим себе электронный аналог демона Лапласа, способного оценив (измерив) состояние каждой ячейки памяти вычислительной системы, предсказать ее состояние на любое число шагов (циклов) вперед. В его роли мог бы выступить просто значительно более мощный компьютер (практическая реализация обычной машины Тьюринга). Загрузив в свою более емкую память текущие данные из исследуемой системы и алгоритм их обработки, он на своем более быстродействующем процессоре просчитал бы (смоделировал) ее дальнейшее поведение. Если у этого демона (назовем его демонов Тьюринга) хватит терпения для того, чтобы просчитать все переходы из каждого состояния, то он смог бы построить полную схему развития системы, фрагмент которой мы схематично приводили ранее (Рисунок 19). Налицо полный фатализм!

Но ответьте, часто ли вы, садясь поработать (или поиграть) за компьютер, выключаете его из-за этой предопределенности? Разве он стал для вас менее интересен после того, как вы узнали о его тотальной детерминированности? Сильно ли вас смущает отсутствие у него невозможности действовать (функционировать) «свободно»?

Думаю, что нет.

Когда мы говорим о нависшем над нашим компьютером фатализме, уместно все же различать предопределенность и предсказуемость. Принципиальное их отличие в том, что подобная полная схема путей развития, будь она построена демоном, не была составлена кем-то ранее, а лишь получилась в результате тщательного анализа составленной кем-то схемы. Система в этом случае детерминирована не из-за навязанного извне сценария, а благодаря детерминированности каждого ее отдельного элемента.

Контраргументация

Как мы знаем, у сегодняшних ученых есть веские основания сомневаться в возможности применимости законов механики Ньютона к описанию всех физических процессов, наблюдаемых во Вселенной. Развитие таких дисциплин, как термодинамика, электродинамика, теория относительности, квантовая теория, синергетика, показало ограниченность этой частной теории. И мне не в коей мере не хотелось бы, чтобы вы подумали, что я хочу «перепеть» старую песню о «вульгарном механицизме» на новый «компьютерный» лад.

Серьезным возражением против изложенной попытки уподобить рассмотренный вариант модели нашего реального Мира, мог бы служить, в частности, вопрос об его изолированности. Действительно, кто сказал, что наша Вселенная не испытывает влияния извне? Другим контраргументом могло бы служить сомнение в возможности точно хранить «реальные» физические данные в цифровой форме. Не допускаем ли мы при этом непозволительные огрубления?

Подобные возражения очень существенны, и я попытаюсь далее представить вашему вниманию и другие модели, которые, надеюсь, смогут расширить проводимые аналогии.

Сейчас же я хотел бы разобраться с другим «популярным» возражением относительно возможности применения точных методов к изучению и описанию окружающих процессов.

Как писал советский философ Пилипенко: «Сведение эволюционного процесса лишь к необходимости, отрицание в нем случайности приводят к концепции механистического детерминизма и к фатализму. Если в биологической эволюции все необходимо, то, значит, она заранее преформирована, детерминирована. В таких условиях в развитии живой природы на протяжении длительных геологических периодов не должно возникать ничего нового. Если все, что происходит сегодня, обусловлено теми же причинами, которые существовали вчера, а люди в прошедшем (вчерашнем) ничего не могут изменить, значит, настоящее, да и будущее, должно развиваться только так, как развивалось прошлое» ([12], с. 162).

Как бы не абсурдна звучала мысль о полной предопределенности развития окружающего нас Мира, подобный детерминизм, на мой взгляд, не является не в коей мере противовесом эволюции. По моему мнению, даже полное исключение случайности не обязательно должно приводить к прекращению появления новых форм эволюционирующих структур.

Шекспир vs шимпанзе

Изолированный цифровой компьютер, несмотря на свою детерминированность, находит широкое применение при решении многих задач и генерирования новых результатов.

Впрочем, эти результаты, вообще говоря, новыми не являются. Это лишь модификация начальных условий. Они не взялись откуда-то извне, а получились благодаря составленному алгоритму при обработке заданных данных. Вот и все!

Посмотрите на замысловатый геометрический узор, представленный ниже (Рисунок 20).

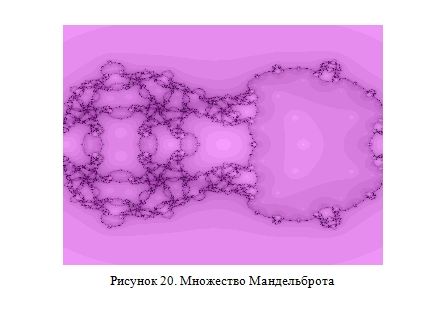
Этот фрактал (множество Мандельброта) получено всего по одной несложной формуле F(c)=c-(c^5-1)/(4c^2) (ну и естественно по заданному алгоритму построения фракталов). Другими словами, этот рисунок есть просто одно из отображений указанной формулы, которая мирно хранится где-то в недрах моего компьютера. Все хитроумные сплетения фрактала, все его точки и линии уже были в этом простом уравнении. А работа программы просто позволила нам несколько по-другому взглянуть на него.

Если представить, что этот рисунок изображен на надутом воздушном шаре, то указанная формула — этот рисунок как бы в миниатюре (когда шарик спущен). Компьютер при этом выполняет роль насоса, надувающего этот шар по заданному закону (программа). А воздух, необходимый для придания шару нужной формы, — это ничто иное, как время, требуемое для перевода его из одного состояния в другое.

Но хотя любой результат (новая идея) есть всего лишь определенная комбинация входных данных (старых идей), тем не менее, подобные решения представляют значительную ценность. Это просто объясняется тем, что они являются крайне редким сочетанием из всего многообразия допустимых вариантов, большинство из которых является самым настоящим «мусором».

Так уж повелось, что кривые, описываемые простыми математическими уравнениями, принято представлять сухими и «безжизненными». И только рука свободного художника способна создать поистине «живое» и красивое творение. Куда там параболе или гиперболе… Отсюда делается логический вывод: красиво только то, что непредсказуемо (случайно); всё, что математически просчитываемо (предсказуемо) — не эстетично. Я ни в коей мере не хочу сказать, что либо против красоты творений мастеров искусства. Просто хотелось бы привести несколько иллюстраций, доказывающих, что и относительно простые (в математическом описании) фигуры способны производить впечатление, на мой взгляд, весьма и весьма эстетическое.

Известна полусерьезная задача, о нахождении вероятности такого события, что сидящая за пишущей машинкой (или компьютером) шимпанзе, наудачу набивая по клавишам, в итоге напечатает без ошибок какое-нибудь произведение Шекспира. Понятно, что такая вероятность хотя и очень невелика, все же отлична от нуля. Ведь подобное произведение представляет собой, по большому счету, ограниченный набор символов. Достаточно посчитать общее количество их комбинаций и выделить из него тот единственный, что соответствует именно этому произведению великого поэта.

Возникает вопрос, а нельзя ли таким образом, просто перебирая все возможные комбинации, получить, в конце концов, требуемое решение? Давайте подумаем.

Во-первых, отметим, что, генерируя каждую комбинацию, мы затрачиваем определенное время (ресурсы). Время так же необходимо и для анализа полученного результата (подходит он нам или нет). Как видим, все упирается во временные ресурсы. Ведь число комбинаций, как было показано, очень резко растет с увеличением размерности решаемой задачи.

В итоге мы получаем следующую ситуацию: метод простого перебора может быть применим для весьма простых задач (таких, как составление слова менее чем, скажем, из семи букв или поиск корней достаточно простой функции на небольшом интервале). Для решения же более сложных задач (написание новых поэм Шекспира или поиск глобального экстремума сложной функции в n— мерном пространстве) не хватит ни вычислительных средств, ни всего отведенного нам времени.

Именно поэтому применяют различные «интеллектуальные» методы поиска желаемого результата. Эти методы идут к нему целенаправленно, сразу отбрасывая множество ненужного «мусора».

Давайте познакомимся с одним из оригинальных методов поиска нужного решения достаточно широкого круга прикладных задач, основанный на имитации эволюционного процесса.

Е-эволюция

Одним из интересных направлений кибернетических исследований конца 80-х годов явилось развитие исследований искусственной жизни (английское название Artificial Life, или ALife). Впрочем, справедливости ради, заметим, что идейно близкие модели разрабатывались еще в 50-70 года прошлого столетия.

Основной мотивацией исследования искусственной жизни служит желание понять и смоделировать формальные принципы организации биологической жизни. К основным эволюционным алгоритмам относятся так называемые генетические алгоритмы, хорошо предназначенные для оптимизации функций дискретных переменных (см.: Росс Клемент. Генетические алгоритмы: почему они работают? когда их применять? [16]).

Эти алгоритмы решают задачи, работая с популяцией из некоторого числа наугад взятых решений. При этом должны быть указаны правила, по котором решения (по аналогии с дарвинской борьбой за существование):

1) скрещиваются (в русской биологической литературе эта операция носит название кроссинговер [crossover]);

2) генерируют потомство;

3) соперничают за ограниченные ресурсы;

4) мутируют;

5) умирают.

Возможные решения представляют в виде двоичных хромосом. Как правило, используют двоичные строки фиксированной длины. Первоначально случайным образом конструируется достаточное множество таких хромосом-решений. Для выяснения того, насколько хорошим результатом они являются, задается специальный алгоритм, вычисляющий их функцию приспособленности, или фитнес-функцию (fitness function).

Фитнес-функция — это единственная часть программы, которая должна понимать, что же на самом деле кодирует хромосома. Соответственно, для каждого приложения следует писать новые фитнес-функции. В остальном же генетический алгоритм является типичным. Мы имитируем выживание сильнейших (survival of the fittest) хромосом. Каждое их последующее поколение выбирается путем стохастической, но целенаправленной селекции. Приспособленность (fitness) той или иной хромосомы-решения определяется как раз указанной фитнес-функцией. Можно ожидать, что качество следующей популяции будет в среднем выше качества предыдущей. То есть более вероятно, что число «хороших» хромосом будет расти, а «плохих» — уменьшаться. Здесь начинают работать факторы эволюции, так как хромосомы фактически вынуждены бороться за место в следующем поколении под действием искусственного дефицита (artificial scarcity).

Для создания новых решений из уже существующих используется такой фактор эволюции, как кроссинговер. При этой операции части двух хромосом, прошедших очередной этап отбора, создают новую. Причем их части не обязательно должны быть одинаковой длины. Точка кроссинговера выбирается произвольно.

Для увеличения вариабельности популяции применяется следующий этап эволюции — мутация (mutation). Ведь даже для больших популяций может оказаться, что не все биты генетического материала в ней представлены. Процесс мутации заключается в инвертировании произвольно взятого бита в очередной хромосоме. Подобное «искажение» гарантирует, что эволюция не зайдет в тупик. Однако, оно должно происходить достаточно редко, дабы не нарушить устойчивость сходимости эволюционного процесса.

Рассмотренные этапы постепенно, шаг за шагом, применяя принцип выживания сильнейшего, «культивируют» достаточно хорошие решения.

Таким образом, мы можем констатировать следующий факт. Изолированный и полностью детерминированный компьютер, обрабатывая достаточно простой алгоритм, на основе начальных «сырых» данных позволяет в итоге получать новые и, главное, практически ценные результаты. Или, проводя аналогии с биологической эволюцией, — мы получаем новые виды в заранее предопределенном Мире.

Здесь можно возразить, что процесс генерации начальной популяции, операция кроссинговера, мутации и выживания требуют, вообще говоря, элемента стохастичности. Однако, в этом случае нам важна не столько сама неопределенность, сколько определенное статистическое распределение некоторой величины. Когда мы ищем точку кроссинговера, нам принципиально не важно, чтобы она появлялась каждый раз по-разному (непредсказуемым образом). Вполне достаточно, чтобы получаемые значения в среднем удовлетворяли, скажем, равномерному распределению, будучи при этом абсолютно детерминированными. А процесс мутации приходился бы, скажем, один раз на тысячу актов отбора популяции.

Понятно, что для подобных целей вполне могли бы подойти рассмотренные ранее псевдослучайные методы генерирования случайных величин: заранее составленные специальные таблицы или датчики псевдослучайных чисел. Эти способы, как было показано, вообще говоря, истинно случайным не являются.

Другое дело, что запущенный таким образом эволюционный механизм будет каждый раз давать один и тот же результат. Но кто сказал, что естественный биологический процесс эволюции, будь он запущен еще раз, дал бы (при прочих равных условиях) результат отличный от нашего?

E-термодинамика

Если бы мы сняли на видеокамеру развитие нашего Мира, а затем прокрутили бы видеопленку назад, то смогли бы отметить два принципиально разных класса событий. Первые, как в прямом, так и в обратном направлении идут качественно одинаково. Траектория упруго отскакивающего теннисного шарика от ровной поверхности, периодические колебания маятника, движение планет в Солнечной системе — все эти процессы являются инвариантными относительно времени. Напротив, такие явления, как растворение капли чернил в стакане с водой или охлаждение только что вскипевшего чайника — таковыми не являются. Процесс кристаллизации одной маленькой капли чернил из подсиненной воды практически не наблюдаем в окружающем нас Мире.

Напомним, что процессы, подобные первым, в термодинамике принято называть обратимыми, а вторые, соответственно, необратимыми. Второе начало термодинамики указывает на возможность самостоятельного протекания в обратную сторону только обратимых процессов, а процессы необратимые способны возвращаться в исходное состояние лишь с участием внешних воздействий. Другими словами, система предоставленная сама себе будет эволюционировать в сторону возрастания внутреннего хаоса — энтропии. В крайнем (предельном) случае этот показатель неупорядоченности останется неизменным. Более строго, энтропия изолированной системы с течением времени не убывает.

Демон Лапласа, будь он способен предсказать будущее состояние обратимого процесса, с такой же легкостью вывел бы и его прошлое, пустив его развитие вспять. Но с необратимыми процессами ему пришлось бы гораздо сложнее: наблюдая, скажем, за водой, налитой в стакане, нельзя определить какое именно ее фазовое состояние предшествовало этому. Ведь это мог быть и лед, и пар, и просто вода. Как говорят в этом случае, система «забывает» свое прошлое состояние.

Посмотрим, как обстоит дело при работе компьютерных программ.

Как мы видели, демон Тьюринга действительно способен просчитать состояние компьютерной системы на любое число шагов вперед. А способен ли он вычислять ее предыдущие состояния? В ряде случаев такую операцию удается выполнить. Пусть, например, действие программы на каком-то шаге ее выполнения заключалось в увеличении содержимого области памяти на единицу. Тогда, имея перед собой модифицированную таким образом группу ячеек и указанный алгоритм, мы (или демон Тьюринга) без особого труда сможем вернуть систему в исходное состояние. Для этого достаточно просто содержимое каждой указанной ячейки уменьшить ровно на единицу.

По аналогии с термодинамикой подобные преобразования назовем обратимыми. Однако большинство изменений в памяти компьютера носят, как правило, необратимый характер. Если, например, программа заменит все единицы из оперативной памяти на нули, то вернуться в исходное состояние, скорее всего, уже не удастся. Ведь до подобной операции в памяти уже могли находиться нули. При этом теряется различие между «старыми» нулями и «новыми» (образованными из единиц). Таким образом, мы наблюдаем деградацию информации, ибо ее неотъемлемым свойством является возможность упорядочивания на основе отличий тех или иных свойств объектов.

Здесь и далее под информацией я буду подразумевать возможность уменьшения неопределенности (энтропии), как это общепринято в теории информации, начиная с работ Клода Э. Шеннона. (В противовес этому — «просто» данные — это потенциальная информация. Они могут ей стать, если мы сможем их правильно интерпретировать. В этом заключается относительность информации: различные наблюдатели могут по-разному оценивать информативность того или иного сообщения. Все зависит от существующего дефицита осведомленности.)

Теория информации

Количественные методы обработки информации были разработаны в 40-х годах XX века в связи с развитием теории информации.

Любое сообщение, с которым мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Очевидно, если бы состояние этой системы было известно заранее, не было бы смысла передавать сообщение. Поэтому в качестве объекта, о котором передается информация, рассматривают некоторую физическую систему, которой заведомо присуща какая-то степень неопределенности.

В качестве меры априорной неопределенности системы в теории информации применяется специальная характеристика, называемая энтропией. Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком.

В качестве основания логарифма берут как правило двойку. При этом единицей энтропии будет являться бит (binary digit).

Анализ состояния памяти компьютера (объемом n бит) в некоторый момент времени можно расценивать как получение сообщения, представленного в виде последовательности из n бит. Если мы не обладали никакими сведениями об ее возможном состоянии, то она имела N=2^n равновероятных состояний, а её энтропия H=n (бит).

После наблюдения за состоянием памяти эта неопределенность будет уменьшена. Чем больше объем полученных сведений, чем они более содержательны, тем больше будет информации о системе, тем менее неопределенным будет ее состояние. Количество информации измеряют уменьшением энтропии той системы, для уточнения состояния которой предназначались сведения. При полном выяснении состояния физической системы приобретаемое количество информации равняется энтропии этой системы: I=H. Таким образом, в нашем случае I=n бит. Именно этим количеством информации потенциально обладает первоначально (до измерения) компьютер с объемом памяти n бит.

Диссипация информации

Возникает вопрос, а что происходит с информацией при последующей работе компьютера?

Нетрудно отметить, что, так как из первоначальных данных, благодаря детерминированной логики работы компьютера, всегда можно вывести его последующие состояния, то «новой» информации мы получить не в состоянии. Обратное же, вообще говоря, не верно. На самом деле, как было показано ранее, не всегда возможно определенно указать предыдущее состояние подобной системы.

Рассмотрим следующий пример.

Пусть алгоритм работы некоторой программы заключается в вычислении n-ого знака в десятичном представлении числа π (пи). На основании заложенного кода компьютер спустя некоторое время выдаст результат. Предположим, что программа никакие изменения (за исключением представления этого результата) в память не вносит. Можем ли мы сказать, что компьютер сгенерировал новую для нас информацию? Действительно, мы не знали, чему равен n— й десятичный знак числа π, поэтому подобный результат, безусловно, привел к уменьшению нашей неосведомленности. Но он был уже предопределен готовым алгоритмом, представленным в виде кода. Работа программы (затраченное процессорное время) позволили лишь представить его в подходящем для нас виде. В этом случае суммарное изменение информации в системе оказалось равным нулю. (Подобный результат представляет для нас ценность в первую очередь благодаря именно затраченным временным ресурсам. Но величина требуемого для расчетов времени напрямую зависит от быстродействия процессора. Следовательно, для более мощного компьютера подобная информативная ценность полученного результата уменьшится. И в переделе может быть всего лишь технологически сведена к величине, близкой к нулю.)

Предположим теперь, что указанная программа во время вычислений использовала основную память для хранения промежуточных результатов расчета. В конце концов, мы также получим результат, плюс потерянную информацию, хранившуюся в этой перезаписанной области. Как следствие информация системы уменьшится.

UnDo

Чтобы быть до конца строгим в своих рассуждениях, рассмотрим такую функцию, предоставляемую многими компьютерными программами, как возможность отката (undo).

Как было показано, многие действия, совершаемые программами над данными, носят необратимый характер. Типичным примером является удаление документа или его фрагмента. Тем не менее, практически все современные приложения позволяют отменить ошибочное действие или целую группу таких операций. Каким же образом это им удается, если мы только что говорили о «забывании» системой своего прошлого состояния?

Технологически подобные программы ведут отдельный журнал производимых действий, в котором сохраняют все данные, необходимые для успешного возврата системы в предыдущее состояние. Понятно, что для ведения подобного журнала необходима дополнительная память, в которой могут храниться ценные данные. Поэтому, сохраняя информацию для одной области, мы столько же (или даже больше) теряем в другой. На лицо аналогия с термодинамикой: уменьшение энтропии отдельной системе, возможно лишь при адекватном увеличении ее в другой системе.

Аналогия 2: Open Universe[3]

Совсем иначе обстоит дело с открытыми (неизолированными) вычислительными устройствами. Внешние, даже незначительные воздействия, накладываясь на детерминированный ход работы процессора, способны привести к появлению случайности на уровне вычислительной системы.

К открытым вычислительным системам относятся аналоговые компьютеры и цифровые машины, так или иначе обменивающиеся с другими устройствами или пользователем. В дальнейших рассуждениях будем иметь в виду именно цифровую неизолированную систему, как аналог Открытой Вселенной.

Если мы построим граф состояний подобной вычислительной системы (Рисунок 21) и сравним его с подобной схемой для изолированного компьютера (Рисунок 19) то отметим появление точек ветвления (бифуркаций).

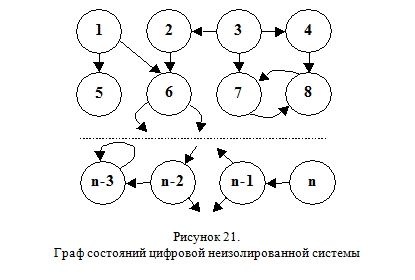
Практически все современные компьютеры и другие цифровые электронные устройства регулярно обмениваются информацией с окружающей их средой. Эта связь обеспечивается благодаря специальным интерфейсам — средствам сопряжения. Алгоритм работы программы (будь то игра, программа для математических расчетов или графический редактор), как правило, существенно зависит от этих внешних потоков информации.

А так как источник этих сообщений не определяется детерминированной логикой компьютера (не входит в его сферу понятий), то результат работы компьютерной программы уже не является предопределенным; хотя последовательность таких сообщений может иметь вполне определенную причинно-следственную связь. Главное, что она не может быть познана в рамках указанной системы.

Выражаясь языком Канта, подобная связь находится за трансцендентной границей. Для обычного персонального компьютера эта граница обусловлена ограниченным набором способов связи с окружающими его предметами и другими устройствами.

Рассмотрим следующий пример.

Пользователь набирает на компьютере текст с книги, лежащей рядом с ним на столе. Поток символов для компьютера является стохастичным, хотя для пользователя он, безусловно, неслучаен. Это показывает относительность случайного.

Предположим, что система «компьютер-программа» решила постараться выявить закономерность в указанном процессе набивания текста. Для этого она могла бы произвести статистический анализ поступающих символов, их взаимную корреляцию и повторяемость. При достаточно длительном наблюдении компьютер смог бы уже выявлять повторяющиеся слова, словосочетания или даже целые предложения. Однако говорить о выявлении им точного закона поведения наблюдаемого явления, понятное дело, не приходится. В данном случае связь с окружающим миром через границу трансцендентности обеспечивается лишь средством принятия информации с клавиатуры.

Представим теперь, что компьютер каким-то образом смог подключиться к внешней цифровой видеокамере. Если она расположена над открытой книгой, то компьютер сможет «видеть» изображение страниц. Возникает вопрос, достаточно ли этого, чтобы он теперь смог заранее предсказать последовательность поступаемых к нему символов?

Отечественный историк и методолог науки Овчиников Н.Ф., критикуя идеи научного детерминизма, приводит следующее возражение: «Допустим, мы поставили себе задачу предсказать на основании научного изучения, скажем, мозга определенного композитора те пятна на нотной бумаге, которые начертит композитор и которые тем самым будут означать предсказание музыкального произведения. Едва ли такая задача разрешима. Аналогично можно заметить и о попытке предсказать какое-либо математическое открытие» ([10], с. 244).

Отчасти, я полностью согласен с приведенным выводом. Действительно, то, что компьютер увидел графическое изображение книги, а, скажем, врач — поверхность мозга пациента, — им ничего напрямую не дает. Компьютер должен быть оснащен специальной программой для распознавания текста. Подобная программа должна уметь правильно интерпретировать видимую картинку в набор символов. Иными словами, убирая лишнее, преобразовывать «сырое» аналоговое изображение в компактный цифровой код. И только эта связка «видеокамера — программа распознавания» способна позволить (с той или иной степенью эффективности) решить компьютеру указанную задачу, несколько «раздвинув» границы трансцендентности.

По аналогии предположу, что наблюдаемые нами необъяснимые явления в окружающем нас Мире, относимые обычно к случайным, возможно суть следствия некой внешней причины, находящейся для нас за трансцендентной стеной. Она обусловлена, в первую очередь, нашими физиологическими и психическими ограничениями. Для познания «потустороннего» Мира нам необходима дополнительная связь с его объектами, плюс умение правильно интерпретировать получаемую информацию. Быть может именно этим и отличаются «просветленные» люди?

На мой взгляд, основная трудность заключается как раз не в отсутствии «видеокамер» или «третьего глаза», а в неумении понять увиденное. К сожалению мы с рождения, будучи ограниченными сложившимися взглядами, законами и предрассудками, привыкаем смотреть на Мир однобоко и предвзято.

Ирландский ученый Уильям Молине (1656-1698) в письме к Джону Локку спрашивал: «Предположим, человек родился слепым и вырос, научившись на ощупь различать куб и шар из одного и того же металла и примерно одинакового размера, т. е. говорить, прикасаясь к этим предметам, какой из них куб, а какой — шар. Предположим теперь, что эти предметы находятся на столе, а слепец прозрел. Сможет ли он, лишь взглянув, но не прикоснувшись к ним, определить, где куб и где шар? (цит. по: [8], с. 266).

Аналогия 3: Квантовая решетка

Устройство современных цифровых компьютеров наделяет их с одной стороны дискретностью (ограниченный набор возможных состояний), с другой — квантованостью по времени (состояние способно измениться только через определенные промежутки времени). Тактовый генератор задает частоту, с которой будет приходить импульс, разрешающий переход в новое состояние.

Не углубляясь в технические детали, будем считать, что и процессор, и память работают на одинаковой частоте в 1 ГГц (10^9Герц). Это означает, что говорить о каком-либо изменении в состоянии такого компьютера можно лишь спустя интервал времени τ=10^-9 с. Это наименьший квант времени для данного устройства. Промежуток времени меньший этой величины попросту недоступен для его восприятия. Задавшись целью, определить для себя, существует ли такой интервал, компьютер столкнулся бы со знакомой нам по квантовой теории парадоксом. С одной стороны этот квант времени не делим (для такого способа восприятия). Но он не делим только для данной конфигурации компьютера, или для программы, работающей на нем. Однако утверждать, что сигнал существует только в дискретные моменты измерения, а между ними «находится в небытие», будет неверно. Это и понятно: природа сигнала никак не зависит от частоты дискретизации компьютера. Другое дело, что выдавать получаемую таки образом картину за истинный сигнал тоже ошибочно. Ведь известно, что через набор точек можно провести множество различных кривых.

Любая связь с внешним миром (через средства сопряжения) заведомо будет осуществляться с частотой, заведомо меньшей тактовой.

Анализируя некоторый физический сигнал (например, через АЦП) с шагом по времени T, программа получила бы ряд точек 1 (Рисунок 22а), а с шагом 2T — ряд точек 2 (Рисунок 22б). Причем первый навлекает мысль о пилообразности сигнала, второй — о его постоянстве.

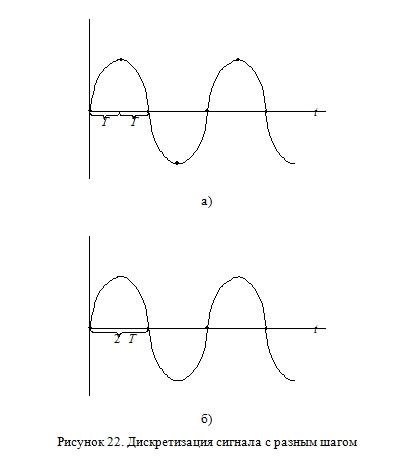
Интересно, что подобный «квантовый эффект» мы наблюдаем при работе с сигналами, имеющими частоту не только большей тактовой частоты компьютера, но и сравнимую с ней. Отдельные программные инструкции выполняются микропроцессором за очень короткий промежуток времени. При работе с относительно медленно меняющимися сигналами такой задержкой можно пренебречь. Но попытка измерить интервал времени T, равный кванту времени τ данного компьютера, вызовет затруднение. Ведь не достаточно получить на входе компьютера сигнал. Самая элементарная операция по дальнейшей работе с ним (запись в ячейку памяти, сравнение, изменение и т. д.) отнимет ресурсы времени никак не меньшие чем τ.

Так как шаг T не может быть меньше времени τ, то если за этот промежуток ситуация во внешнем мире изменится существенно, то компьютер столкнется с проблемой «неадекватности восприятия реальности». Возможно, что-то подобное мы наблюдаем при попытке работать в квантовом масштабе пространства и времени.

В любом случае, утверждать что-либо о значении сигнала между актами измерения можно будет лишь по косвенным признакам: производя дополнительные замеры, суммируя объем информации и производя затем интерполяцию.

Иными словами, «по мере возрастания сложности системы наша способность формулировать точные, содержащие смысл утверждения о ее поведении уменьшается вплоть до некоторого порога, за которым точность и смысл становятся взаимоисключающими.

Этот принцип несовместимости связан со способом восприятия и рассуждений человека. В его основе лежат обобщенные, схематизированные, а, следовательно, неточные субъективные представления о реальности» ([6]).