Глава 1. Основная классификация компьютеров

Современные компьютеры по основному закону, лежащему в основе их работы, можно разделить на несколько групп. В контексте нашего разговора о генерировании случайности целесообразно выделить следующие типы вычислительных машин: аналоговые, цифровые и квантовые.

Разберем каждый из этих типов подробно. Это необходимо в первую очередь для того, чтобы понять, почему так сильно отличается процесс генерирования случайности на каждом из них. В дальнейшем это поможет нам выявить некоторые аналогии с моделями окружающего нас Мира.

Аналоговые компьютеры

Аналоговые компьютеры — это класс устройств, в которых непрерывные переменные типа электрического напряжения, давления жидкости, механического движения представлены в компьютере в аналогичной (непрерывной) форме. То есть решение будет представлено в виде сигналов, имеющих ту же природу, что и решаемая задача.

Аналоговая система настраивается согласно начальным условиям и затем эволюционирует во времени. Результат снимается путем измерения переменных непосредственно в аналоговой модели.

В этом случае, ряд входных величин (Рисунок 1) взаимодействует между собой в специальном устройстве (звене) по какому-либо фундаментальному закону. Например, это может быть взаимодействие электрического контура с магнитным полем или зависимость мгновенного напряжения на конденсаторе от силы тока в цепи. Аналоговый компьютер представляет собой совокупность таких звеньев, каждое из которых описывается некоторой передаточной функцией — зависимостью выходной величины (результата) от входных (начальных условий).

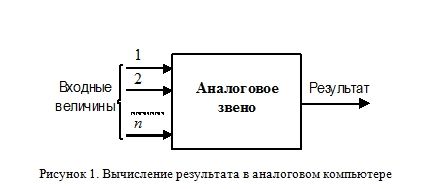
Работа современных электронных аналоговых компьютеров основана, в основном, на измерении разности потенциалов. Они построены на операционных усилителях — устройствах, на выходе которых, генерируется ток, пропорциональный разности потенциалов на входе. На основе таких усилителей может быть реализован широкий класс математических операций, включая инверсию, суммирование, дифференцирование и интегрирование. Типичный электронный аналоговый компьютер состоит из многочисленных типов усилителей, которые могут быть сконфигурированы таким образом, чтобы создать соответствующую математическую модель, иногда большой сложности, с множеством переменных.

Аналоговые компьютеры особенно хорошо подходят для моделирования сложных динамических систем, так как такое моделирование может выполняться, как правило, в реальном времени. Они широко использовались при расчете самолетов, атомных электростанций, промышленных химических процессов. Другой областью их применения является анализ гидравлических сетей (например, потока жидкости через систему коллектора) и сложных электрических цепей (например, для расчета очень протяженных цепей).

Поскольку производство интегрированных чипов для цифровых компьютеров стало гораздо проще и дешевле, чем создание аналогичных цепей для аналоговых компьютеров, аналоговые и гибридные компьютеры постепенно были вытеснены дискретными вычислительными машинами. Впрочем, гибридные компьютеры в ряде случаев продолжают быть полезными и поныне, используя свои аналоговые процессоры как средство сопряжения с реальным миром.

Цифровые компьютеры

В этом счислении существуют всего лишь два обозначения — 0 и 1,

с помощью которых можно записать все числа.

Позже я обнаружил, что оно выражает также логику дихотомий,

польза от которых величайшая…

Лейбниц. «Рассуждения о религии и философии в Китае»

В отличие от аналоговых, цифровые компьютеры работают только с дискретными данными. Все переменные в независимости от их природы (будь то давление жидкости, напряжение или сила тока) должны быть предварительно переведены в цифровую форму. Другими словами, цифровые компьютеры при расчетах имеют дело с абстрактной моделью, имеющей дискретное (как правило, двоичное) представление.

В принципе, аналоговые компьютеры также моделировали изучаемую систему или процесс, представляя, скажем, явление теплопередачи разностью потенциалов. Но степень абстракции в дискретных вычислительных машинах несравненно выше.

Машина Тьюринга

Все существующие на сегодняшний момент цифровые компьютеры могут быть смоделированы так называемым клеточным автоматом Тьюринга. Это детерминированная и дискретная машина.

Формально она представляет абстрактное устройство, состоящее из:

— конечного алфавита из символов;

— бесконечной ленты, разделенной на квадраты, в которых записаны эти символы;

— ограниченного множества внутренних состояний;

— читающей головки, подведенной к одному из квадратов ленты.

Программа для машины Тьюринга представляет набор правил, по которым, в зависимости от состояния машины и содержимого текущего квадрата, выполняются следующие действия:

— в текущий квадрат на место старого символа записывается новый, и машина переходит в новое состояние;

— головка перемещается в соседний квадрат, и машина так же переходит в новое состояние;

— машина останавливается.

Начальные данные для программы — слово, записанное на ленте в момент включения машины. Результат работы — слово, возникшее на ленте после остановки машины.

Фон-неймановская машина

В 1949 году американский математик Джон фон Нейман высказал концепцию, которая положила начало современной обработке данных. Он предложил идею интегрирования рабочей программы в память машины в закодированном виде. Нейман дал следующее описание функционального принципа компьютера: «В нем есть процессор, который напрямую связан с памятью, где данные и (или) программа находятся наготове для обработки. И они обрабатываются в процессоре друг за другом».

Первая ЭВМ с хранимой программой получила название EDSAC (Electronic Delay Storage Automatic Calculator — электронный калькулятор с памятью на линиях задержки). Она была создана в Кембриджском университете (Англия) в 1949 году. С тех пор все ЭВМ являются компьютерами с хранимой программой.

Фон-неймановская вычислительная машина, по сути, представляет собой одну из практических реализаций машины Тьюринга.

Перечислим основные принципы ее функционирования:

1. Машина состоит из: блока управления, арифметическо-логического устройства (АЛУ), запоминающего устройства (внешняя память), устройства ввода-вывода (интерфейс).

2. Программа и данные хранятся в одной и той же памяти (концепция хранимой программы).

3. Устройство управления и арифметическо-логическое устройство (обычно объединенные в центральный процессор) определяют действия, подлежащие выполнению, путем считывания команд из оперативной памяти.

Иными словами, машина Фон-Неймана представляет собой активный блок (центральный процессор), взаимодействующий путем интерфейса (устройства сопряжения) с пассивной памятью (Рисунок 2), хранящей данные и инструкцию для их обработки (программу).

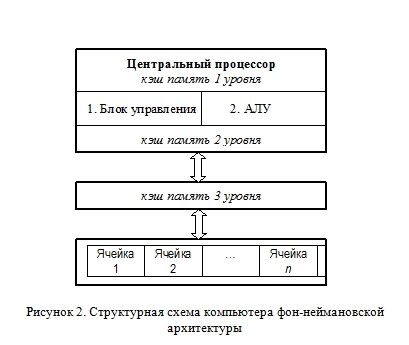
Процессор включает в себя набор регистров — внутренних переменных, над которыми он способен быстро выполнять операции. Количество регистров и их формат может существенно меняться от одной конкретной модели к другой.

Так для оптимизации обработки данных и, как следствие повышения производительности, практически все современные вычислительные машины оснащены быстрой кэш-памятью. Такая относительно небольшого объема память служит своего образа буфером между центральным процессором и более медленной оперативной памятью. Однако на логику работы компьютерной программы кэш-память влияния не оказывает, так как является прозрачной для нее.

Программа для фон-неймановской вычислительной машины состоит из набора команд, которые проверяются одна за другой. Операции, выполняемые процессором, включают в себя следующие элементарные манипуляции с данными:

— считывание информации из ячейки с заданным адресом в регистровую память процессора;

— логические и арифметические операции над данными;

— запись информации в указанную ячейку.

По существу, на таких «примитивных» действиях и основана работа любых современных приложений, будь то графический редактор, игра или программа решения математических задач, на цифровых ЭВМ.

Изначально цифровые компьютеры создавались как абсолютно детерминированные устройства для быстрой и безошибочной обработки некоторого набора данных, строго согласно заданному сценарию. Действительно, основой логической работы любого компьютера был и остается алгоритм — заранее заданная последовательность четко определенных правил или команд для получения решения той или иной задачи (например, путем выполнения некоторой вычислительной процедуры) за конечное число шагов.

Определение слова компьютер, данное в русском переводе второго издания (1986 г.) английского словаря “DictionaryofComputig” издательства “Oxford University Press” [13], остается и, пожалуй, останется актуальным.

• «computer — Компьютер, ЭВМ. Устройство или система, способная выполнять заданную, четко определенную последовательность операций. Это чаще всего операции численных расчетов и манипулирования данными, однако сюда относятся и операции ввода-вывода; операции внутри последовательности могут зависеть от конкретных значений данных».

За предшествующие годы компьютеры изменились очень сильно, но это развитие явилось все же эволюцией. Революция свершилась гораздо раньше: в 30-40-е года, когда выбор был сделан в пользу цифровых, а не аналоговых вычислительных систем. Фоннеймоновская архитектура, машина Тьюринга, двоичное кодирование — все это до сих пор сохранило актуальность на фоне чрезвычайно стремительного развития технических средств. Изменилась форма, но содержание осталось практически прежним.

Таким образом, мы видим, что основным принципом функционирования любого современного компьютера является его детерминированность. Сама его суть не совместна с понятием случайность. А как иначе? Мы должны быть уверены, что программа, выполненная правильно 10 раз подряд правильно, будет выполнена точно также и на 1000, и на 1001 раз. В противном случае, теряется сам смысл ее функционирования. Любая случайность, такая как помеха, погрешность, непредвиденный сбой или нарушение работы рассматривается как аварийная ситуация.

Выбор, сделанный в середине XX века, в пользу цифровых ЭВМ как более перспективных по сравнению с аналоговыми, был обусловлен их большей помехоустойчивостью и, как следствие, точностью. То есть, записав в память такого компьютера некоторую программу или данные, мы должны быть уверены, что ни эта программа, ни результаты ее работы не будут подвержены влиянию каких-либо внешних, нежелательных, случайных воздействий. Такую возможность могли предоставить лишь ЭВМ на базе дискретных элементов, с ограниченным набором устойчивых состояний. Хотя электронные вычислительные машины на такой базе, по сравнению со считавшимися тогда традиционными аналоговыми, во многом другом им проигрывали. И в первую очередь в связи с необходимостью значительного увеличения числа конструктивных элементов (например, в запоминающем устройстве). Действительно, для адекватного (в рамках решаемой задачи) представления аналоговой по природе величины в цифровой форме, необходим достаточно большой объем дискретизации.

Например, в некоторых аналоговых ЭВМ, вывод результата вычисления (скажем, решения обыкновенного дифференциального уравнения) заключался в повороте специальной рамки с током на определенный угол. Наблюдателю оставалось измерить величину этого угла поворота. Понятно, что такой метод был, во-первых, весьма длительным (инерционным), а, во-вторых, не точным. На окончательный результат влияла как погрешность измерения, так и внешние неконтролируемые возмущения. То есть, выполняя точно такие же расчеты повторно, мы могли бы получить несколько другой результат. Такие компьютеры можно считать открытыми системами, на результат работы которых, оказывает влияние внешняя (по отношению к ним) среда.

В цифровых же компьютерах результат любого расчета представляется совокупностью достаточно большого числа отдельных элементов. Причем каждый из них обладает лишь небольшим набором состояний. Вследствие чего его работа становится гораздо более устойчивой и надежной. Следует отметить, что вышеуказанное не означает, что такой элемент физически не может находиться не в каких других состояниях, кроме специально определенных. Просто весь ряд его возможных состояний логически делится специальным образом на те или иные зоны (интервалы). Нахождение элемента внутри этого интервала расценивается как одно и то же состояние. И оттого, что физическое состояние элемента вдруг незначительно изменилось (из-за каких-либо случайных факторов) его логичное состояние останется для наблюдателя прежним. Размер таких интервалов (и их число) выбирается из расчета, чтобы практически все неконтролируемые возмущения не выводили элемент за эти условные границы. Благодаря такой избыточности, поведение элементов и, как следствие, всей системы можно сделать сколь угодно невосприимчивой к неинформационному шуму и исключить случайную составляющую в ее работе.

В примере с вращающейся рамкой мы могли бы использовать несколько таких рамок и под каждой из них специальный круг, разбитый на интервалы (секторы). А отсчет результата вести уже не по углу поворота, а в какой сектор этого круга указала ее стрелка. Теперь малое случайное отклонение рамки (вызванное, например, легким ветром) не приведет к искажению результата, если размер секторов выбран с достаточным запасом. Итак, выигрывая в точности, мы вынуждены усложнять структуру вычислительной машины.

Другими словами, здесь абсолютно справедлив принцип «разделяй и властвуй», сформулированный еще Александром Македонским, когда вместо того, чтобы работать с одним сложным элементом, мы пытаемся рассматривать поведение большого числа простых.

В современной электронной технике в качестве таких элементарных частей используются бистабильные элементы, то есть элементы, которые способны находится всего в двух устойчивых состояниях (скажем, «0» или «1»). Это вызвано тем, что такие устройства являются наиболее устойчивыми и надежными по сравнению с полистабильными (с числом состояний более двух). Вследствие этого такая форма представления сигналов называется двоичной. Одним из сдерживающих факторов при переходе со старой аналоговой к такой цифровой архитектуре было как раз неудобство хранения и работы с такой двоичной формой с позиции человека. Столь привычная для нас десятичная система счисления не очень подходит для цифровых ЭВМ. Однако очевидный выигрыш в точности и быстродействии предопределил дальнейшую тенденцию к развитию именно цифровых вычислительных машин. Вся вторая половина XX века показала правильность такого выбора. Успехи микроэлектроники позволили перейти от медленных и громоздких электрореле и ламп к миниатюрным и быстродействующим транзисторам. Это привело к созданию (и постоянному усовершенствованию) маленьких, быстродействующих и дешевых компьютеров с большими массивами надежной памяти. С другой стороны, развитие программной индустрии позволило пользователям и программистам в той или иной степени абстрагироваться от неудобной («неестественной») двоичной формы представления данных.

Квантовые компьютеры

Алиса попыталась вообразить, на что похоже пламя свечи,

когда свеча погасла, но это ей не удалось, —

ведь, к счастью, ей этого никогда не приходилось видеть.

Льюис Кэрролл. «Алиса в стране чудес»

В общих словах, квантовый компьютер — это система, собранная из микроскопических элементов, которая подчиняется законам квантовой, а не классической механики (В качестве материала при составлении данного обзора использованы статьи из источников Михаил Вялых. Ключевые слова: квантовые вычисления [18], Егор Кобылкин. Квантовые кубики [18], Юрий Романов. Y++ [20] и Дан Медовников, Владимир Тюменев. Считающий атом [21]).

Благодаря проявлению определенных квантовых эффектов (например, принципу суперпозиции), в квантовом компьютере реализуется естественный параллелизм, недоступный классическим компьютерам. При этом в процессе вычислений происходит параллельная обработка сразу всех возможных вариантов комбинаций решаемой задачи.

Практическая реализация такого компьютера, позволяющая решать сколько-нибудь практически полезные задачи, на данный момент пока еще отсутствует. По прогнозу ряда специалистов говорить всерьез об эре квантовых компьютеров можно будет не ранее 2010 года.

Поэтому на данном этапе приходится говорить лишь о более или менее сформировавшейся теоретической базе.

Российский математик Юрий Манин еще в 1980 году высказал предположение, что квантовый шум, который в ходе миниатюризации микросхем неизбежно превратится в препятствие для их нормальной работы, можно попытаться использовать для конструирования компьютеров нового типа, считающих по новым, квантовым алгоритмам.

В 1982 году Ричард Фейнмам (Richard Feynman) написал статью, в которой рассмотрел два вопроса. Он подошел к процессу вычисления как физик: есть ли какое-нибудь физическое ограничение на функционирование компьютера, которое накладывает некие запреты на реализуемость алгоритмов? Он показал, что термодинамических ограничений, типа второго начала термодинамики, нет. А значит, уменьшая потери энергии и шумы, вычисления можно сделать обратимыми. Далее он обратил внимание на то, что если у нас имеется квантовое устройство, то есть подчиняющееся квантовой механики, то его вычислительные возможности совершенно не должны совпадать с возможностями обычного устройства.

В 1985 году Дэвид Дойч (David Deutsch) из Оксфордского университета дал определение того, что такое квантовый алгоритм.

Решающий шаг сделал в 1994 году исследователь из BellLaboratories Питер Шор (Peter Shor), придумав первый эффективный квантовый алгоритм для дискретного логарифмирования. Достаточно сказать, что эта задача считается настолько сложной для обычных классических вычислительных машин, что многие криптографические протоколы основаны именно на трудности его отыскания.

Вскоре коллега Шора Лов Гровер (Love Grover) показал, что квантовые вычисления гораздо эффективнее классических не только при взломе шифров, но и при поиске в неупорядочных базах данных большого размера.

Вспомним классические эксперименты квантовой оптики, наглядно демонстрирующие волновые свойства квантов света — фотонов. Впрочем, результаты опытов с точностью до условий проведения справедливы для всех микрочастиц.

В опыте №1 между источником света и экраном (чувствительная фотопластина) имеется ширма с двумя отверстиями (Рисунок 3а). Если источник света монохроматический, то можно получить на экране характерную интерференционную картину, вызванную небольшой разностью фаз пучков света, проникающих сквозь отверстия.

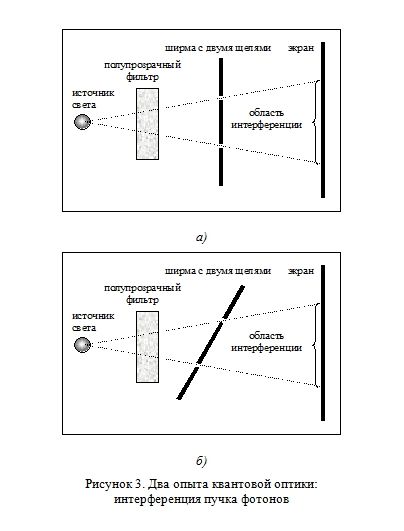
Будем теперь снижать интенсивность источника света, до тех пор, пока не получим последовательность одиночных летящих в сторону экрана частиц, так чтобы в каждый момент времени в объеме установки присутствовал всего один фотон. Если представлять его как упругий шарик, то интерференционная картина должна прекратиться. Однако на практике этого не происходит — узоры остаются.

Отсюда делается вывод, что фотон обладает способностью, двигаясь к экрану, проходить одновременно через два и более отверстия, а в более общем случае — движется к нему одновременно всеми возможными путями.

В опыте №2 (Рисунок 3б) ширма с отверстиями немного наклонена. При такой конфигурации получается, что фотон либо проходит сквозь ближайшее отверстие, либо через дальнее, но не через оба одновременно. Действительно, не может же он, пройдя одно отверстие, затем «вернуться» и пройти через другое? Опыт показывает, что в каком то смысле может. То есть фотон следует считать не только чем-то большим, протяженным поперек пути следования, но и распределенным, «размазанным», занимающим определенный объем даже вдоль своего пути.

Основным элементом квантового компьютера являются квантовые биты, или кубиты (от Quantum Bit, qubit). Обычный бит — это классическая система, у которой есть только два возможных состояния. То есть пространство состояний бита — это множество из двух элементов (например, нуля и единицы). Кубит же — это квантовая система с двумя возможными состояниями (например, электрон, у которого спин может быть равен либо -½, либо +½). Другим словами, кубит — это двумерное комплексное пространство.

Квантовый компьютер — это система, собранная из кубитов, которая подчиняется законам квантовой механики. В ней можно выполнять так называемые унитарные преобразования пространства состояний такой системы. Это такой класс воздействий на квантовую систему, при которых не теряется записанная в кубит информация и не нарушается когерентность волновых функций кубитов.

Для квантовой системы, согласно законам квантовой механики, справедлив так называемый принцип суперпозиции. Его можно сформулировать так: если имеется система, которая может находиться в каких-либо двух состояниях, то она может оказаться и в состоянии, называемом их линейной суперпозицией. Состояния удобно представлять себе как векторы в некотором пространстве — его обычно называют фазовым пространством. Таким образом, суперпозиция — это линейная комбинация векторов в фазовом пространстве, с произвольными комплексными коэффициентами (амплитудами).

Для системы, имеющей дискретные степени свободы можно выделить так называемые базисные векторы, определяющие ее чистое состояние, то есть такое состояние, которое можно непосредственно наблюдать. Помимо него существует и множество состояний, в котором такие комбинации присутствуют одновременно с той или иной вероятностью, но сказать что-либо определенное о них до момента измерения мы ничего не можем.

Для описания поведения квантовых систем было введено понятие волновой функции (ψ-функции). Существуют волновые функции, называемые собственными для какой-то конкретной измеряемой величины. В состоянии, описываемом собственной функцией, значение этой величины может быть точно предсказано и до ее измерения. Однако квантовая система может находиться и в состоянии с волновой функцией, равной линейной комбинации собственных функций, соответствующих каждому из возможных значений.

Описанные выше эксперименты с ширмой позволяют ясно увидеть, что в пространственной структуре одной единственной частицы (или, более строго, — в структуре ее волновой функции) можно записать очень много информации и даже создать условия, в которых информация будет обрабатываться заданным образом, однако в результате всех этих действий на выходе будет получена волновая функция, хотя и содержащая всю необходимую информацию, но способную проявить себя лишь в одном-единственном взаимодействии.

В нашем примере структура волновой функции каждого фотона в области за ширмой несет в себе информацию обо всех отверстиях в ширме, об их конфигурации и форме, оптической плотности и т. п. Однако каждый фотон «отметился» на экране только в одной точке (в акте взаимодействия с фотоэмульсией).

Квантовый процессор можно построить с использованием даже одной-единственной микрочастицы, и он будет работать и давать результаты. Но воспользоваться им не удастся: ведь, по одной точке или букве текста трудно понять, о чем идет речь в книге.

При объединении двух квантовых систем результирующее фазовое пространство будет определяться тензорным произведением, а его размерность будет равна произведению размерностей исходных систем. В этом заключается принципиальное отличие квантовых систем от классических, в которых размерности складываются, и получаемая система представляет собой декартово произведение (имеет вид кортежа: «состояние первой системы, состояние второй системы»).

Согласно квантовой механике, до тех пор, пока квантовая система эволюционирует под действием унитарных операторов, мы не можем сказать в каком именно классическом состоянии она находится. Только в результате измерения, переводя ее в чистое состояние, мы сможем определить это с некоторой степенью вероятности. Математическая формализация такой процедуры измерения имеет следующую интерпретацию: в фазовом пространстве фиксируется некоторый базис, по которому разлагается вектор состояния системы. Вероятность получения того или иного результата представляет собой квадрат модуля коэффициентов разложения.

Таким образом, чтобы получить необходимо достоверный результат, понадобится раз за разом воспроизводить исходное состояние квантовой частицы и выполнять все преобразования — получая на выходе все новые и новые реализации процессов измерения. Другими словами, в этом случае, мы занимаемся накапливанием статистики.

Налицо противоречие: либо мгновенный ответ, но с бесконечно большой вероятностью ошибки, либо — абсолютно точный, но требующий бесконечно долгий срок.

Из-за того, что для представления информации используются кубиты, в которых как бы записано сразу оба значения — и 0, и 1, в процессе вычислений происходит параллельная обработка сразу всех возможных вариантов комбинаций битов. Таким образом, в квантовом компьютере реализуется естественный параллелизм, недоступный классическим компьютерам.

Как было сказано, все существующие на сегодняшний момент обычные (не квантовые) компьютеры, даже с параллельной обработкой информации на многих процессорах, могут быть смоделированы клеточным автоматом Тьюринга. С возникновением и обсуждением идей квантовых вычислений стала активно развиваться квантовая теория информации и, в частности, теория квантовых клеточных автоматов. Квантовый клеточный автомат является обобщением автомата Тьюринга для квантовых компьютеров.

Практическая реализация квантовых компьютеров усложняется их высокой чувствительностью ко всякому роду внешним возмущениям.

Кубиты находятся в некоем смешанном состоянии, причем согласованно-смешанном. Их набор представляется когерентными волновыми функциями. Благодаря этому, после прохождения через квантовый процессор, использующий унитарные преобразования, волновые функции кубитов заставляют интерферировать друг с другом, наблюдая получающуюся картину и судя по ней о результате вычисления.

В каком-то смысле квантовый объект — это одна большая квантовая частица, обладающая способностью одновременно проявляет себя во множестве взаимодействий, число которых в пределе равно количеству элементарных компонентов (ψ-функций), из которых объект построен.

В отличие от унитарных преобразований любое другое воздействие на когерентную квантовую систему, которое позволяет получить информацию о кубитах системы, разрушает их когерентность. Такая потеря когерентности часто происходит и без обмена энергией с окружающей средой и даже только при попытке самой проверки когерентности.

В заключение приведу любопытный отрывок из статьи Юрия Романова в журнале «Компьютерра» (Юрий Романов. Y++ [20]).

«Практическая работа над созданием квантовых вычислителей неминуемо приведет материалистов к пониманию того, что материя нашего Мира не есть совокупность “частиц-кирпичиков мироздания”, но представляет собой нечто более общее, доступное наблюдению лишь косвенно — через те или иные ее проявления, которыми, в частности, являются микрочастицы и их совокупности — предметы.

Идеалистам придется смириться с тем, что в Мире все же ничего нематериального нет. И информация — последний оплот и надежда мистиков — есть только свойство материи, пусть даже такой необычной, как та, что стоит за привычными микро— и макрочастицами».