Разберемся, чем вызвана потребность получения случайных чисел на компьютере. Существует, по крайней мере, три области, где такое генерирование необходимо. Перечислим их в порядке повышения требований, предъявляемых к «качеству» получаемых таким образом чисел.
1. Программы, интерактивно взаимодействующие с человеком (программы-агенты, компьютерные игры и т. п.).
2. Программы, предназначенные для решения определенного класса математических задач, так называемые недетерминированные задачи (например, численный метод Монте-Карло).
3. Программы для шифрования информации (криптография).
Интерактивные программы
Затем он [микропроцессор ЭВМ] может выдать код,
соответствующий данной ошибки,
чтобы пользователь мог найти ее в своем руководстве.
В более дружественных системах может сообщаться еще
и характеристика ошибки, например SYNTAX ERROR…
«Ориентированный на пользователя — дружественный (user-friendly)».
Dictionary of Computing. Oxford University Press. 1986
Существует целый ряд программ, призванных помогать людям в некоторых относительно «интеллектуальных» областях их повседневной деятельности, будь то сбор информации, ее анализ и прогнозирование: эдакие «персональные агенты» или «персональные ассистенты». Человек, пользующийся такой программой, желает иметь не просто инструмент для «бездумного» перемалывания горы данных, но «личного» помощника, умеющего делать это «разумно» и быстро, а в качественном отношении не хуже, чем он сам. Другими словами, пользователь хочет видеть достойного, ему подобного собеседника. А так как люди отличаются некоторой, порой весьма выраженной, нелогичностью своих действий и суждений, то не удивительно, что они привыкли наблюдать это и у окружающих. Поэтому жестко ограниченное, строго вычислимое поведение электронного «собеседника» будет «резать глаз», значительно уменьшая впечатление «человечности» общения. А так как сегодняшние технологии еще не позволяют говорить всерьез об искусственном интеллекте, то единственным простым способом сделать такие программы более или менее «человечными» является искусственное добавление в них доли нелогичности, то есть элементов случайности. Такая их характеристика будет хоть как-то эмулировать некоторые черты поведения человеческого поведения и примитивным путем создавать иллюзию некой разумности.
Разберемся, почему так происходит.
Понятно, что более сложные системы ведут себя более сложно и менее предсказуемо с позиций некоторого наблюдателя. Действительно, для относительно простой системы можно попытаться удержать в голове закон ее поведения и взаимодействия с другими системами. Для более сложных систем в силу усложнения такого поведения и появления ряда новых, это становится практически невозможным. С другой стороны, чем более сложной является система, тем к более «разумной» ее, как правило, относят. Поэтому, в первом приближении, можно наблюдать следующую корреляцию: всё что просто и предсказуемо — неразумно, разумно же то, что сложно и непонятно.
Устройства, умеющие выполнять ограниченный набор задач по строго заданному алгоритму, вряд ли смогут быть названы разумными с точки зрения человека, насколько сложной не была бы их внутренняя конструкция. Современный холодильник, начиненный серией микропроцессорных устройств, поддерживающий оптимальный температурный и влажностный режимы, может быть назван, в лучшем случае, «интеллектуальным» устройством (и то в кавычках). Даже если такой агрегат будет приветствовать вас каждое утро открытием дверцы, и напоминать о заканчивающихся продуктах, он все равно останется набором металла. И только если он научится чувствовать наше настроение, если он будет способен интуитивно предсказывать наши желания, если, наконец, он начнет капризничать и ворчать, пожалуй, только тогда мы примем его в свою касту существ разумных, ибо он спустился до наших слабостей. А так как до сих пор нет четкого определения таких понятий как «чувствовать» или «интуитивно предугадывать», то, увы, любое примитивное устройство, способное хоть каким-либо образом вызывать у нас подобные ассоциации, может до поры до времени претендовать на роль «разумного».
В данном случае мы говорим о компьютерных программах — программах, которым «ничего человеческое не чуждо».
В область таких программ следует по праву отнести практически все известные компьютерные игры. Действительно, компьютер в этом случае выступает в роли соперника, достойного самого человека. Такая игра предполагает последовательность вызовов человеку, на каждый из которых он должен дать, по возможности, максимально достойный, оптимальный ответ. Именно поиск такого оптимума, в большинстве случаев и доставляет удовлетворение в подобных играх, будь то правильный ход фигуры в шахматах, или точный выстрел в игре-«стрелялке». Понятно, что вызов, на который уже был однажды выбран оптимальный ответ, в дальнейшем существенно теряет интерес к себе. Поэтому в идеале игра должна представлять собой бесконечную последовательность неповторяющихся эпизодов. Принимая для каждого из них решения и видя результат своих действий, человек включается в цепь обратной связи. Обучаясь на своих ошибках (отклонениях текущего результата от желаемого), он стремится к определенной цели: как можно сильнее их минимизировать. Неважно, что здесь является подобным отклонением: проигрыш партии в шахматы или выигрыш на двадцать первом ходу, а не на двадцатом.
Однако любая компьютерная игра рано или поздно заканчивается, после чего мы вынуждены запустить ее вновь с начала. Если она не изменяет сценарий своего поведения, то уже вскоре наскучит нам. Человек не инвариантен по отношению ко времени и память о прошлой игре не даст нам получить такое же удовольствие, беспрестанно играя в одну и ту же игру с одним и тем же сценарием.
А так как никто не хочет выпускать «одноразовые» игры, то отсюда следует единственный выход: позволять играм вести себя каждый раз, в той или иной мере, по разному, не линейно.
В первую очередь, достичь этого можно благодаря «нелинейности» самого человека. Действительно, так как любая компьютерная игра интерактивна, то человек, как нелогическое звено в системе «человек-игра» способен каждый раз заставлять ее генерировать новый сценарий. Скажем человек, в одной из шахматных партий, может начать игру так, а в другой уже по-другому. Понятно, что дальнейшая партия при этом будет развиваться уже совсем по иному сценарию. Однако, этого недостаточно. Действительно, человек вправе ожидать, что сценарий будет различным, даже если он будет играть каждый раз одинаково. Иначе игроку опять же будет неинтересно.
Введя в алгоритм программы пусть даже небольшой элемент случайности, можно избежать подобных недостатков. Если позволить компьютеру случайно выбирать, скажем, в одном из десяти случаях не самый оптимальный, а просто локальный оптимальный ход, то уже скоро ход развития партии предсказать будет невозможно.
Решение математических задач специальными численными методами
Есть люди, полагающие, что математика —
это нудное занятие, которое всегда уныло и скучно;
мы же находим математику развлечением
и не стыдимся признаться в этом.
К чему проводить четкую грань между делом и игрой?
Дональд Кнут. «Конкретная математика»
Первоначально компьютеры (или, как их тогда называли — ЭВМ — электронно-вычислительные машины) создавались именно для математических расчетов. Существует класс задач, к решению которых целесообразно применять так называемые недетерминированные методы. Наиболее известным из них является метод Монте-Карло (Впервые метод был систематически изложен в 1949 году американскими учеными Н. Метрополисом и С. Уламом) для численного интегрирования функций (приближенного нахождения определенных интегралов). Такие методы требуют генерирования большого количества чисел, удовлетворяющих специальным законам распределения случайной величины.
Криптографические алгоритмы
Вообще криптография — дисциплина о разработке приемов и методов перевода сообщения в шифр и обратного его восстановления при наличии специального электронного ключа. Такой ключ представляет собой просто последовательность чисел, как правило, значительно меньшую, чем само шифруемое сообщение.
Существует две основные модификации такого шифрования:
— криптография с открытым ключом (асимметричные алгоритмы);
— криптография с «секретным» ключом (симметричные криптографические алгоритмы).
Мы не будем вдаваться в детали (подробнее см., например, [19]), однако отметим, что и в том и в другом случае требуется, как правило, необходимость частого повторного генерирования первоначального ключа. Понятно, что оттого насколько он будет уникален, зависит надежность дальнейшего шифрования. Это опять же требует возможность генерирования случайных чисел на компьютере.
Сравнение и анализ
Все три рассмотренные задачи существенно отличаются требованиями, предъявляемыми к генерированию случайных чисел.
Скажем, в первом случае (игра в шахматы) нет никакого строгого ограничения на «качество» получаемых чисел для внесения элемента случайности при выборе оптимального хода. Игроку, по большому счету, абсолютно не существенно каким именно алгоритмом пользовался компьютер, выбрав из двух равновероятных ходов тот, а не другой.
Гораздо более строго дело обстоит с третьим рассмотренным случаем (криптография). Здесь крайне необходимо, чтобы совокупность генерируемых чисел строго удовлетворяла заданным условиям и чтобы они были обязательно случайными. От первого условия зависит степень «зашифрованности» сообщения, то есть стойкость шифра к попыткам взлома. Второе условие гарантирует невозможность просто определить сам шифр. По аналогии с обычным замком мы требуем, чтобы, во-первых, был крепок его механизм, и, во-вторых, было бы сложно подделать к нему ключ.
Более необычно дело обстоит во втором случае (решение математических задач методом Монте-Карло). Здесь при различном наборе случайных чисел мы будем получать, вообще говоря, различные результаты расчетов. Поэтому такие числа также должны удовлетворять определенным, строго заданным условиям (распределениям). Только в этом случае мы можем быть уверены (с некоторой степенью вероятностью), что полученное решение верное (мы имеем в виду задачи, имеющие единственное решение).
Однако, от таких чисел, вообще то, говоря, и не требуется, чтобы они были случайными! Необходимым условием является лишь, то чтобы вся совокупность таких чисел удовлетворяла заданному статистическому распределению случайной величины. А из этого вовсе не следует, что все числа, ее составляющие, действительно случайны каждый по отдельности.
Скажем, событие наступления извержения вулкана Санторин на острове Тира мы, пожалуй, можем назвать абсолютно случайным. Но вряд ли оно может быть полезным при решении указанных задач, в силу редкости наступления. С другой стороны, набор цифр: 3, 1, 4, 1, 5, 9, 2, 6, 5, 4… кажется на первый взгляд тоже случайным, но представляет собой всего лишь запись известного числа π (пи) и может быть заранее предсказан (вычислен) с любой необходимой точностью. Однако он может вполне подойти для решения тех же математических задач в силу того, что совокупность этих цифр, скорее всего, удовлетворяет требуемому распределению случайной величины.
Практическая реализация
С точки зрения математики, на первый взгляд, все кажется достаточно просто. Мы просто ищем подходящее случайное событие и используем каким-либо образом получаемые случайные величины в своих целях.
Однако на практике все оказывается значительно сложнее.
Рассмотрим это на примере компьютеров, отметив, что такая реализация существенно зависит от типа используемого компьютера, точнее от фундаментальной природы используемого в их функционировании процесса.
Генерирование случайности
Проблема получения случайных чисел на аналоговом и квантовом компьютерах решается достаточно просто, можно сказать, «сама собой».
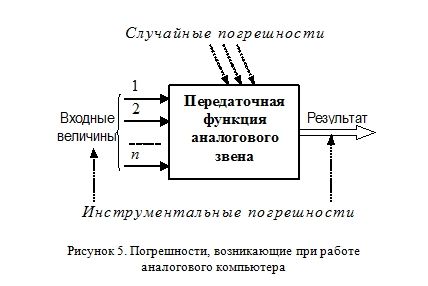
Процесс вычислений на аналоговом компьютере можно изобразить в виде условной схемы (Рисунок 1). Компьютер такого типа выступает в роли открытого (взаимодействующего с окружающей средой) устройства (Рисунок 4) и подвержен ряду внешних воздействий, приводящих к возникновению различного вида погрешностей (Рисунок 5).
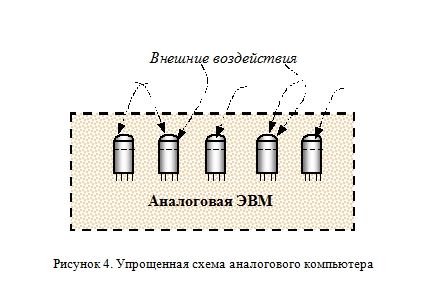
Из-за несовершенства измерительных приборов мы не можем подать на вход аналогового компьютера абсолютно точное значение непрерывной величины. Также мы не способны точно измерить результат (выходной параметр) вычислений. Такие погрешности принято называть инструментальными. Далее, аналоговый компьютер, являясь полностью не изолированным от воздействий внешней среды, подвергается на протяжении всей своей работы влиянию случайных погрешностей из окружающего пространства.
В случае квантового компьютера дело обстоит еще более сложно.
До тех пор, пока квантовая система эволюционирует, мы не можем точно сказать в каком состоянии она находится. Только в результате измерения, переводя ее в чистое состояние, мы сможем определить это с некоторой степенью вероятности. Иными словами, в фазовом пространстве фиксируется некоторый базис, по которому разлагается вектор состояния системы. Вероятность получения того или иного результата представляет собой квадрат модуля коэффициентов разложения.
Таким образом, правомочно говорить об объективно существующей случайности в обоих типах таких компьютеров. Другое дело цифровой компьютер. В этом случае мы имеем систему максимально защищенную от внешнего нежелательного воздействия (Рисунок 6).
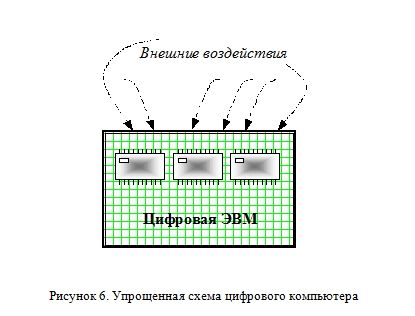
Внутренние процессы в цифровом компьютере происходят по «классическим» детерминированным законам, без «углубления» на квантовый уровень. Тем не менее и для цифровых компьютеров существует несколько приемов получения последовательностей случайных чисел. Рассмотрим три основных метода:
1. Использование специализированных внешних устройств, генерирующих случайные числа.
2. Использование таблиц случайных чисел.
3. Применение датчика псевдослучайных чисел.
Специализированные внешние устройства
Как правило, в роли таких устройств выступают некоторые внешние по отношению к компьютеру приборы, усредняющие результат поведения достаточно большой системы неких элементов. Каждый из элементов ведет себя, быть может, по вполне детерминированному, но весьма сложному закону. Когда же мы рассматриваем результат их взаимного наложения, то он становится еще более сложным.
Для аналоговых вычислительных машин с этой целью часто использовали «шумы» в электронных лампах: если за некоторый фиксированный промежуток времени уровень «шума» превысил заданный порог четное число раз, то записывается нуль, а если нечетное число — единица.
Более совершенной конструкцией является использование внешнего прибора, регистрирующего число распавшихся атомов некоторого изотопа за определенный промежуток времени. Как известно, нельзя точно предсказать, когда распадется тот или иной отдельный атом: мы можем лишь статистически описывать их большую совокупность (например, значение такого параметра как период полураспада).
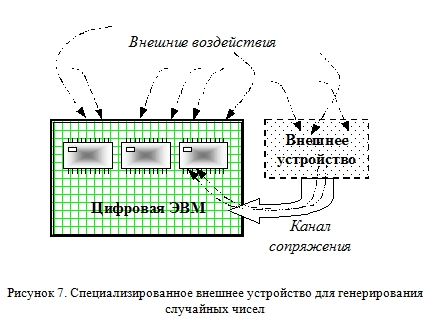
В этом случае при необходимости сгенерировать случайное число, компьютер обращается через специальное средство сопряжения к внешнему прибору и получает от него усредненный результат совокупного поведения множества некоторых элементов. Характер поведения этих элементов и форма усреднения выбирается с целью получения ряда случайных чисел, принадлежащих определенной совокупности.
Итак, к дискретному детерминированному компьютеру мы добавили некоторое звено, которое можно считать аналоговым и стохастическим (Рисунок 7). При этом результат генерируется не самим компьютером, а специальным внешним устройством. Получая все новые и новые числа, мы можем быть уверены, что они никак не коррелируют (не связаны) с процессами, протекающими внутри ЭВМ.
К недостаткам этого метода следует отнести:
1. Конструктивная сложность такого прибора. Действительно, возникает необходимость приобретения дополнительного, возможно достаточно дорогого и сложного внешнего прибора. Требуется так же его сопряжение с компьютером.
2. Мы должны быть уверены, что различные устройства будут генерировать «похожие» случайные числа. То есть закон распределения должен быть неизменен независимо от того, какое конкретно устройство мы используем и с каким компьютером оно соединено.
Вообще, такие устройства использовались на заре развития ЭВМ, но не нашли широкого применения как раз из-за указанных недостатков. Уже давно используются другие методы получения случайных чисел: по заранее составленным таблицам и с использованием, так называемых, датчиков случайных (псевдослучайных) чисел.
Таблицы случайных чисел
Идея такого метода заключается в следующем. На специально сконструированном устройстве один раз производится генерирование некоторого достаточно большого набора случайных чисел. Устройство сконструировано таким образом, что полученная совокупность удовлетворяет заданному закону распределения (полученный набор тщательно проверяется специальными статистическими методами анализа). На его основании составляется таблица случайных чисел или, другими словами, упорядоченный набор чисел, гарантированно удовлетворяющий определенному типу распределения. Единожды составленная (и статистически проверенная) такая таблица может быть затем многократно использована для решения определенных прикладных задач. Действительно, зачем заново проводить сложные испытания на специальном оборудовании, если можно воспользоваться ранее составленными качественными данными? Однако следует отдавать себе отчет, что хотя получаемые данным образом числа и соответствуют требуемому закону распределения, по существу, не являются истинно случайными. Ведь существует принципиальная возможность заранее предсказать весь набор таких чисел, либо наблюдать повторение этой последовательности при повторном или многократном ее использовании.
Достоинства в реализации метода:
1. Отпадает необходимость в дополнительном постоянном устройстве генерирования случайных чисел. Вместо серийного выпуска таких генераторов создаются единичные (пусть и относительно дорогие) приборы. При этом отпадает необходимость его сопряжения с компьютером и жесткая унификация (стандартизация).
2. Точность получаемого результата. Ведь дополнительно к качеству генерирования прибора добавляется строгий статистический анализ получаемой последовательности с целью выявления нежелательного отклонения от требуемого распределения.
Однако на этом все преимущества табличного варианта, пожалуй, заканчиваются и начинаются недостатки:
1. Ограниченный набор случайных чисел. При их исчерпании придется использовать их повторно, что может быть крайне не желательно.
2. Необходимость в постоянном хранении массива данных. Понятно, что большие таблицы занимают много места в запоминающем устройстве компьютера. Это было особенно актуально, когда объем памяти большинства ЭВМ был очень (по сегодняшним меркам) небольшим.
3. Невозможность получения истинно случайных последовательностей. Это главный недостаток таких таблиц с позиции получения случайных чисел. Действительно, любая таблица представляет собой упорядоченную последовательность элементов. И одна и та же таблица всегда будет начинаться с одних и тех же чисел. И хотя их совокупность возможно и будет удовлетворять статистическим критериям случайного распределения, каждое число по отдельности будет находиться в строго определенном месте этой таблицы и при последовательном просмотре будет появляться отнюдь не случайно, а строго после предшествующего элемента.
Поэтому, чтобы гарантировать абсолютную случайность такой таблицы необходимо соблюсти как минимум три условия:
1. Ее объем должен быть достаточно большим для решаемой задачи, чтобы не пришлось использовать ее повторно.
2. Сама таблица должна содержаться в секрете при работе с ней.
3. Для каждого нового сеанса необходимо использовать новую таблицу.
В криптографии, где требования к «качеству» случайных чисел максимально строги, применение всех трех указанных требований не редкость. Такие методы получили название одноразовые шифры. Они действительно могут (при правильном их применении) гарантировать стопроцентную теоретическую степень защиты от преднамеренного взлома любыми криптоаналитическими методами (Такая абсолютная степень защиты была математически доказана известным математиком, основателем теории информации Клодом Шенноном в 30-х годах. Действительно, при наложении секретного ключа, имеющего длину, равную (или большую) длине исходного (открытого) сообщения, в получаемом шифре теряется отличие между этим ключом и шифруемым сообщением.)
Для не таких критически важных областей применения выполнение всех этих требований весьма обременительно. Поэтому на практике, когда математик, вооруженный бумажной таблицей хочет получить из нее новый набор случайных чисел для решения некоторой численной задачи, он поступает приблизительно следующим образом. Закрыв глаза, наугад указывает в ее произвольную область и выбирает число, на которое случайно попал. Так повторяется до тех пор, пока не будет выбрано необходимое количество. В этом случае вполне правомерно говорить о случайном наборе случайных чисел, если сам процесс выбора считать достаточно случайным (несмотря на его субъективность). Но во внутренней работе цифрового компьютера мы не можем представить себе такой выбор «наугад». Как уже говорилось, любое действие строго детерминировано и вполне определенно в зависимости от предыдущего состояния. Чтобы выбрать случайным образом число из такой электронной таблицы мы должны воспользоваться, например, еще одной аналогичной таблицей. Но для того, чтобы этот выбор был случаен, мы опять же будем вынуждены прибегать к услугам еще одной подобной таблицы и так далее до бесконечности. В конце концов, мы приходим все же к необходимости хотя бы один раз (на начальном уровне) произвести лишенный случайности («обдуманный») выбор. Другими словами, изолированный от внешних воздействий цифровой компьютер не сможет сгенерировать действительно случайное число. Мы можем долго усложнять алгоритм работы программы, вырабатывающей случайные числа, но не до бесконечности. А раз так, то в любом случае ее действие можно будет представить как последовательное выполнение конечного числа строго детерминированных операций. И результат готового алгоритма будет полностью определяться входным параметром (начальным условием). А так как, включая компьютер, мы переводим его каждый раз в одно и тоже начальное состояние, то становится ясным теоретическая невозможность решения такой задачи.
Итак, все более усложняя алгоритм работы генерирующей программы, мы не решаем основной проблемы, но получаем ситуацию, когда отпадает необходимость в самой таблице случайных чисел! Такой метод получил название датчика псевдослучайных («почти» случайных) чисел.
Датчики псевдослучайных чисел
Первый алгоритм для получения чисел таким образом был предложен Дж. фон Нейманом. Он назывался методом середины квадратов. Поясним его на примере.
Пусть задано 4-х значное число. Возведем его в квадрат, в результате чего получим уже 8-значное число. Выберем средние четыре цифры этого числа, возведем уже их в квадрат и снова извлечем четыре средние цифры. И так далее.
Метод середины квадрата не оправдал себя: получалось больше чем нужно малых значений. Так 62 числа вырабатывают последовательности, которые вырождаются в 0,0000, 0,0000, 0,0000, …; 19 чисел — в 0,0010, 0,0010, 0,0010, …; и т. д.
Для задач криптографии важно, чтобы генераторы псевдослучайных чисел были воспроизводимыми, хотя в тоже время они должны вырабатывать числа, которые кажутся случайными. На основании теории групп было разработано несколько типов таких датчиков. В настоящее время наиболее доступными являются конгруэнтные генераторы ([9]). На основе их строгого определения можно сделать математически корректное заключение о том, какими свойствами должны обладать выходные сигналы этих генераторов с учетом периодичности и случайности.
Основные достоинства общего метода генерирования случайных чисел методом датчика псевдослучайных чисел по сравнению с табличным — отказ от необходимости использования специальных громоздких массивов данных. Хорошо составленный алгоритм, по существу, как бы «воссоздает» шаг за шагом аналог такой таблицы. То есть вся таблица (потенциально бесконечная) как бы хранится в «сжатом» виде (в форме относительно небольшого алгоритма плюс начальное условие). Благодаря быстродействию компьютеров такой метод вытеснил табличный уже давно.
Недостаток у датчика псевдослучайных чисел тот же, что и у табличного метода: генерируемая цепочка чисел полностью определяется начальным параметром (и используемым методом генерирования).
Именно поэтому моделируемые величины называют псевдослучайными. С одной стороны совокупность достаточно их большого числа ведет себя как совокупность «настоящих» случайных величин. Но при более тщательном рассмотрении начинает проявляться их взаимозависимость. При одинаковых начальных условиях будут генерироваться идентичные цепочки чисел. Впрочем, это свойство для некоторых задач является приемлемым и даже полезным. В частности на стадии разработки алгоритма при решении ряда математических задач численными методами удобно иметь возможность генерировать одну и ту же последовательность случайных чисел для его отладки и анализа. А в криптографических задачах даже необходимо, чтобы однажды полученная цепочка чисел (при шифровании данных) была воспроизводима в дальнейшем (при расшифровывании).
Фактор времени
Программисты, разрабатывавшие программы в то «далекое» время, когда основным языком программирования был ASSEMBLER, могут поправить меня, что я не рассмотрел еще один метод получения случайных чисел на ЭВМ: используя некоторые так называемые служебные параметры компьютера. Это такие системные параметры работы ЭВМ, как число записанных/прочитанных байтов с внешнего устройства, количество выделенной памяти, коэффициент загрузки процессора и другие. Для всех компьютеров прежней конфигурации таким параметром было время, прошедшее с момента включения электропитания.
На всех машинах PC и PS/2 входной генератор для микросхемы системного таймера имеет частоту, равную 1,19318 мегагерц (1 МГц = 1 000 000 Гц) или 1 193 180 циклов в секунду. На более ранних компьютерах эта частота была возможна меньше, но получить число хотя бы десятков миллисекунд было вполне возможно. Тогда, при необходимости смоделировать случайное число, скажем целое и равномерно распределенное в интервале от 0 до 99, программист может поступить, вставив в программу команду, получающую, к примеру, две последние цифры в количестве миллисекунд, прошедших с момента включения компьютера. Будучи простым, этот метод хорошо себя оправдывал, если такие числа генерировались не слишком часто и не периодически. То есть когда промежуток времени между получением случайных чисел значительно (на порядки) превышал квант времени системного таймера и был не строго постоянен. В противном случае будет наблюдаться ощутимая корреляция (зависимость). Разберемся, отчего это происходит.
Обозначим число квантов времени, прошедших с момента включения компьютера как функцию времени f(t). Понятно, что такая функция (Рисунок 8) будет во-первых линейной, а во-вторых дискретной (в силу цифрового устройства компьютера).
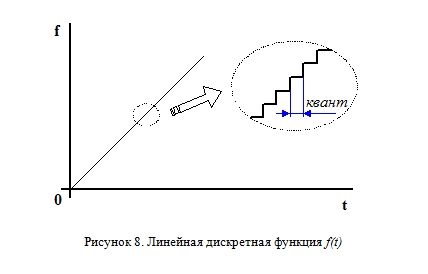
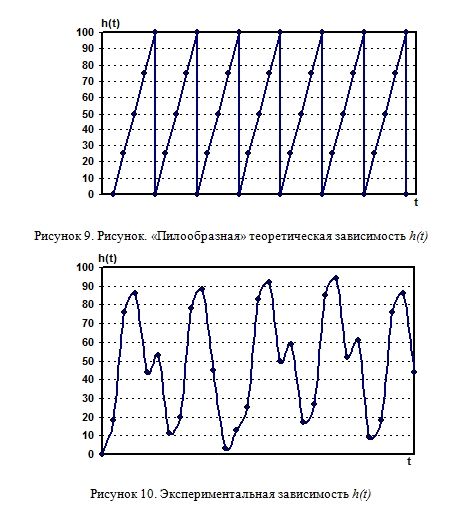
Если же мы будем рассматривать две последние цифры этой функции, то получим аналогичную зависимость h(t), но ограниченную верхним пределом, равным 100. Такая функция, во-первых, описывается известным (и достаточно простым) законом, а, во-вторых, периодическая. Поэтому для получения случайных чисел через регулярные промежутки времени она не подходит: получаемая таким образом последовательность так же будет периодичной (точки, помещенные на Рисунок 9).
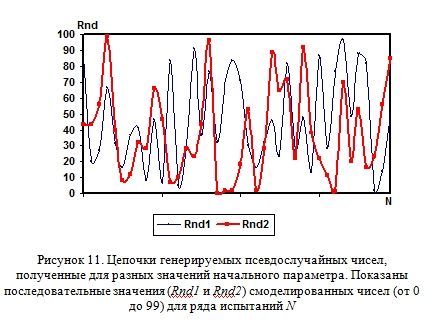
Это подтверждает моделирование такого процесса на ЭВМ (Рисунок 10 — для удобства полученные точки соединены плавными линиями). (Расхождение с теоретической зависимостью объясняется, по-видимому, в первую очередь, грубостью существующего алгоритма отсчета тиков (ticks) в операционной системе компьютера. Такая точность отсчета в PC-совместимых машинах, доступная в языках высокого уровня (на уровне операционной системы, без использования специальных средств работы с портами) составляет всего 1/65536 от возможной частоты (генерируемой кварцевым генератором), т. е. около 55 миллисекунд.)
Раз последовательность получается периодичной, то на практике часто применяют следующий прием. К такой функции времени обращаются один раз — для запуска датчика псевдослучайных чисел. В этом случае датчик, запущенный на одну, скажем, миллисекунду позже или раньше, начнет генерировать уже другую последовательность чисел. А так как при повторном запуске программы вряд ли удастся соблюсти такую точность, мы будем получать каждый раз все новые и новые цепочки случайных цифр (Последовательности Rnd1 и Rnd2, смоделированные на компьютере и показаны на Рисунке 11).
На первый взгляд задача решена только внутренними силами компьютера. Однако давайте разберемся, какую роль здесь играет категория время. Следует давать себе отчет, что абсолютное время, то есть хранящееся в энергонезависимой памяти ЭВМ (скажем 12:00 по Гринвичу) является внешним фактором по отношению к его внутренней логике. Действительно, от компьютера не зависит в какое конкретное время его включили. Это событие было обусловлено другими факторами, внешними по отношению к нему.
С другой стороны, относительное время, то есть хранящееся в некоторой ячейке оперативной памяти компьютера и показывающее сколько тактов прошло с момента его включения является уже внутренним параметром.
Казалось бы, этот параметр считать случайной величиной никак нельзя. Однако здесь мы наблюдаем ситуацию, когда на этот параметр накладывается некий внешний фактор, а именно время, прошедшее с момента от запуска компьютера до обращения. Это событие было так же обусловлено чисто субъективными обстоятельствами человека, являющегося в данном случае внешней системой по отношению к компьютеру. Понятно, что он не сможет специально запустить программу точно в одно и тоже время, ибо погрешность его действий будет не сопоставима с длительностью кванта времени, используемого в генераторе компьютера.
Выводы
Итак, мы рассмотрели основные способы получения случайных чисел на компьютере и пришли к выводу: получить случайное число для изолированного от внешнего воздействия цифрового компьютера невозможно. Задавая одни и те же начальные условия, мы получим идентичное поведение компьютера — и никаких случайностей. И лишь добавим к его работе внешние (по отношению к нему) неконтролируемые им воздействия, мы сможем говорить об элементе случайности. То есть случайность — явление, присущее лишь системе, взаимодействующей с другой системой, функционирующей независимо от нее.


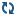












Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.
Если вы используете ВКонтакте, Facebook, Twitter, Google или Яндекс, то регистрация займет у вас несколько секунд, а никаких дополнительных логинов и паролей запоминать не потребуется.