Глава 3. Аналоговое или дискретное

Мы не будем восстанавливать историю развития и формирования взглядов философов и физиков на устройство нашего мироздания от Демокрита до Лейбница и далее. Попытаемся лишь кратко разобраться в сегодняшнем положении дел.

Основные отличия Аналога и Цифры

Разделение всех явлений и процессов на непрерывные (аналоговые) и прерывистые (дискретные) кажется весьма очевидным. Действительно, есть явления, которые ведут себя однородно, плавно, и состоят, на первый взгляд, из бесконечного числа элементов. Напротив, системы, которые образованы отдельными, хорошо различимыми компонентами, делимы уже не до бесконечности и ведут себя, как правило, скачкообразно (квантовано). (Вопрос о том, делимы ли сами элементы этой системы, в данном случае нас не интересует по той причине, что на этом уровне абстракции мы в качестве системы рассматриваем именно набор этих компонентов, а не каждый элемент в отдельности. Примером может служить обычный песок. Хотя, в первом приближении, его масса ведет себя, словно непрерывная консистенция, на самом деле она состоит из конечного множества отдельных крупинок. Причем, говоря об этой совокупности крупинок, мы не затрагиваем вопрос о делимости каждой частички в отдельности.)

Так, с позиции здравого смысла, мозаика, составленная из даже пусть очень большого (но конечного) числа разноцветных стеклышек — дискретна, а картина, написанная масляной краской — непрерывна. Однако все становится не так просто, когда мы начнем рассматривать мозаику издали, в результате чего отдельные составные части ее сольются; а картину с очень близкого расстояния (или даже при помощи микроскопа), когда можно будет разглядеть дискретные частички краски.

На самом деле есть множество примеров, когда действительно дискретные системы или явления представляются в силу субъективного восприятия аналоговыми. Не будем далеко ходить за доказательствами.

Обычная телепередача, транслируемая по телевизору, представляется в конечном виде в дискретной форме (причем весьма грубой). Изображение, видимое нами на экране (в статике) составлено из матрицы отдельных точек, причем их число не так уж и велико (менее 1 000 по вертикали и горизонтали). Более того, показ передачи (динамика изображения) дискретна и во времени. Частота смены кадров составляет всего несколько десятков в секунду. Другими словами, смена набора из порядка одного миллиона точек 24 раза в секунду создает у зрителя устойчивое впечатление непрерывного действия. Субъективизм такого восприятия станет еще более заметным, если вспомнить, что те же пчелы будут воспринимать такой фильм все же, как последовательность отдельных кадров, так как такой частоты дискретизации для них недостаточно.

На мой взгляд, понятие непрерывность, напрямую связанное с понятием бесконечность, является все же более математической абстракцией, нежели физически существующей реальностью. Действительно, как будет показано ниже, даже в «чистой» математике определение «бесконечность» имеет весьма размытый смысл. Известный специалист по теории бесконечных множеств и основаниям математики А. Френкель писал: «Преодоление пропасти между областью дискретного и областью непрерывного, или между арифметикой и геометрией, есть одна из главных, — пожалуй, даже самая главная проблема оснований математики… Характер рассуждений теперь, конечно изменился, но трудности, как и прежде, возникли в связи с пропастью между дискретным и непрерывным — этим неизменным камнем преткновения, играющим в то же время чрезвычайно важную роль в математике, философии и даже физике» (Цит. по [4], с. 12-13).

Представление пространства и времени в виде протяженных и непрерывных субстанцией приводит к ряду парадоксов. Такие противоречия известны с античных времен. Рассмотрим два из них.

Первый связан с непрерывностью пространства и известен, как парадокс Зенона. При таком положении дел, скажем, стрела, пущенная из лука, не сможет двигаться, так как перед тем, как пролететь половину своего пути, она должна сначала пролететь половину от этой половины и так далее до бесконечности. Другими словами, стрела должна иметь бесконечную скорость, чтобы переместиться на бесконечное (делимое до бесконечности) пространство.

Второй парадокс (парадокс Ахиллеса) вызван представлением времени, как непрерывной категории. Суть его в следующем. Быстроногий Ахиллес, имеющий скорость большую, чем неторопливая черепаха, тем не менее никогда ее не догонит. Действительно, пока он пробежит путь, первоначально разделявший их, черепаха уже сместится на некоторое расстояние, которое бегун будет вынужден вновь преодолеть, но за это время она вновь переползет вперед и так далее. Рассуждая таким образом, мы делаем вывод, что Ахиллес на каждом этапе будет сокращать дистанцию между ним и черепахой, но реально никогда ее не догонит.

Подобных парадоксов можно вполне избежать, если предположить дискретность пространства и времени. Действительно, в первом случае стрела на своем пути должна пролететь не бесконечное число положений, а пусть и очень огромное, но все же ограниченное их число. Следовательно, ее скорость не обязана быть бесконечно большой.

Во втором случае Ахиллес догонит черепаху, как только промежуток времени, необходимый ему, чтобы сократить расстояние, разделяющее их, станет меньше определенного кванта времени, неделимого уже на части.

Почему мы не замечаем подобную дискретность пространства и времени? Только из-за того, что эти категории имеют настолько малые кванты, что мы не способны их воспринимать. Для нас они как бы сливаются. То есть отличие аналогового от дискретного следует искать в количественном отношении.

В этой связи представляет интерес пример с развитием компьютерной техники.

Действительно, вычислительные машины двадцати и даже десятилетней давности представлялись само собой как дискретные системы. А как иначе? Достаточно было взглянуть на монитор, чтобы понять это: отдельные крупные литеры, каждая строго в своей позиции экрана. Более того, каждая из них сама состояла из видимых невооруженному глазу точек (пикселов). Распечатка текста или графического изображения на матричном принтере также состояла из видимого растра.

Вычислительная мощность компьютеров очень быстро росла, и за несколько лет разрешение картинки на экране монитора и на современных лазерных и струйных принтерах сравнялась и по четкости, и по цветности[1] с физиологическим разрешением органов восприятия человека. То есть дальнейшее повышение подобного качества уже не столь замечается глазом (и мозгом) человека. Как следствие, сейчас рядовые пользователи воспринимают компьютер скорее как непрерывную (аналоговую) систему. Хотя цифровые вычислительные машины по прежнему остались строго квантованными как по разрешению, так и по времени. Действительно, кроме того, что вся память компьютеров состоит из ограниченного набора дискретных запоминающих элементов, так и процесс обработки данных происходит через определенные кванты времени. Другими словами, компьютер способен выполнять инструкции отдельно друг от друга лишь по одной за такт. Поэтому говорить об «истинной» мультизадачности в процессе выполнения программ не приходится. Процессор способен лишь быстро переключаться с одной задачи на другую, создавая иллюзию их непрерывного одновременного исполнения.

Что же потребовалось, для перехода компьютеров из разряда дискретных в разряд «непрерывных»? По большому счету, всего лишь стократное увеличение объемов памяти и тактовой частоты электронных компонентов. На мой взгляд, впечатляющий пример перехода количества в качество при усложнении количества всего на два порядка.

Другими словами, и это мое глубокое убеждение, отличие между аналогом (непрерывностью) и цифрой (дискретностью) состоит только в количественном отношении. Аналогом следует считать такую дискретность, когда влиянием ее отдельных составляющих становится возможным (в рамках решаемой задачи) пренебречь.

Винил и домены

Можно привести целый ряд примеров, когда множество известных цифровых по сути приборов субъективно относят к аналоговым. С дискретностью таких «аналоговых» устройств, как фотоаппараты (как цифровые, так и пленочные) или музыкальные и видео-диски (CD, DVD и т. п.) все более или менее понятно. Рассмотрим предположение о дискретности такого, уж казалось бы «истинно» аналогового процесса, как запись музыки на «классическую» магнитофонную ленту.

Действительно, даже у специалистов существует устоявшееся мнение, что такая запись качественно отличается от цифровой (на том же проигрывателе лазерных дисков). Однако вот что пишет по этому поводу один из постоянных авторов компьютерного еженедельника «Компьютерра»:

«Преимущества аналоговых магнитофонов и проигрывателей виниловых пластинок очевидны далеко не для всех. Несколько читателей справедливо отмечают, что так называемые аналоговые ленточные магнитофоны по своей сути являются цифровыми устройствами. Дело в том, что число магнитных доменов, попадающих в зазор звукоснимающей магнитной головки, конечно. Читатели предполагают числа от 16 000 до 100 000 (точные данные не известны). Но, в любом случае, это относительно небольшое число и уж точно это не бесконечность. А домены имеют всего два устойчивых состояния намагниченности. Таким образом, магнитная головка, по сути, есть ЦАП (цифро-аналоговый преобразователь) с конечной разрядностью от 14 до 17 бит и высокочастотным интерполирующим фильтром низкой частоты (его образует система магнитная головка-зазор-лента), возможно, дополнительно увеличивающим разрядность до 18-19 и даже 20 бит.

Из сказанного выше следует, что мы просто не можем слышать чисто аналоговых записей, так как ленточные магнитофоны применялись и при создании виниловых пластинок. А значит, со старого доброго “винила” тоже идет цифровой звук! Поэтому когда утверждают, что «аналоговый» звук лучше цифрового, на самом деле утверждается, что одна цифровая система лучше другой!» (Дмитрий Симаненков. Загадки и парадоксы цифрового звука [17]).

В противовес этому редактор вышеуказанного журнала Михаил Брауде-Золотарев пишет следующее:

«Я категорически не согласен с тезисом о дискретности пленочных магнитофонов. Да, магнитные домены дискретны. Да, они имеют всего два состояния намагниченности. Но цифровым воспроизведением от того все равно не становятся… Посудите сами: домены ориентированы в пространстве случайным образом вокруг доминирующего направления непрерывно, и, следовательно, снимаемый с них сигнал не дискретен. Его значение меняется в пределах между +U и — U, определяясь проекцией направления домена на звукоснимающую головку, измеряющую поле с сотен тысяч доменов одновременно. Это дает статистически очень сильное усреднение, полностью скрывающее “дискретность” доменов. А после этого остаются шумовые факторы, сопровождающие снятие звука с пленки, в виде толщины магнитного слоя, собственных шумов магнитной головки и т. п., в свою очередь лишающие сигнал всяких признаков дискретности. (Кстати, идея о дискретности пленочных магнитофонов вызывает у меня такую ассоциацию: попытка измерять высоту самолета, летящего на высоте нескольких километров с точностью до сантиметров, игнорируя тот факт, что самолет в полете попадает в воздушные ямы, что меняется рельеф местности и т. п.)» (Дмитрий Симаненков. Загадки и парадоксы цифрового звука [17]).

Эти доводы мне представляются в основном правильными и достаточно убедительными. Однако такое возражение не опровергает, а, напротив, в чем, то даже подтверждает мое высказанное предположение о количественном различии непрерывного и дискретного. На самом деле, оттого, что мы не имеем возможность измерить высоту самолета с точностью до сантиметров (или даже микрон), вовсе не означает принципиальную непрерывность пространства. А именно о таких принципиальных (а не инструментальных) вопросах я пытаются рассуждать в этой книге.

Здесь я более солидарен с Сергеем Леоновым (другим редактором еженедельника «Компьютерра»): «А ведь и “ламповый” звук является квантованным, учитывая дискретность отдельных летящих от катода к аноду электронов. Так же, как не является истинно аналоговым и звук, записанный на спиральной дорожке состоящего из дискретных молекул и атомов винила. И вообще не существует никакого “аналогового воспроизведения” — кто сказал, что ток в обмотке звуковой головки не то же самое квантование с точностью до перепрыгивающих по орбитам электронов?

Выходит все дело в величинах. И закон Мура в интерпретации для обрабатываемых в единицу времени данных сулит нам не что иное, как бесконечное приближение к полному “аналогу”. Точнее, к той “цифре”, которую мы будем считать “аналогом”» (Сергей Леонов. Бесконечное приближение [15]).

Теория множеств

Если тебе трудно понять всю бесконечность, постарайся понять ее хотя бы на половину.

Славомир Врублевский

Рассмотрим теперь отличия дискретного и непрерывного с более абстрактной позиции, а именно, с позиции раздела математики — теории множеств. Напомним вначале определения основных классов чисел.

Натуральными называются числа вида 1, 2, 3,… и так далее.

Целыми являются числа из последовательности …-3, -2, -1, 0, 1, 2, 3,…, т. е. положительные натуральные, отрицательные натуральные и число нуль.

Числа, представимые в виде дроби p/q, где p и q — целые числа и q≠0, принято называть рациональными.

Соответственно числа, которые невозможно представить в такой форме, относят к классу иррациональных чисел.

Совокупность всех рациональных и иррациональных образует множество действительных (вещественных) чисел.

Понятно, что каждый последующий класс из последовательности натуральные — целые — рациональные [иррациональные] — действительные включает в себя предыдущие. Отдельно множество иррациональных чисел принято подразделять на алгебраические и трансцендентные.

Первые являются корнями (решениями) некоторого алгебраического уравнения n-ого порядка с рациональными коэффициентами. Соответственно трансцендентные числа решениями подобных уравнений не являются.

В математике часто приходится иметь дело с подобными наборами каких-либо элементов. Раздел, имеющий дело с такими совокупностями, называется теорией множеств.

Само понятие множество не может быть определено через другие более простые характеристики. Оно является, по сути дела, аналогом (синонимом) таких слов как набор, коллекция, совокупность. Ключевой характеристикой понятия множество является отсутствие заданного места у элементов, его образующего.

Итак, множество — совокупность неупорядоченных элементов. При этом нельзя говорить о позиции (порядковом номере) какого-либо элемента в данном множестве. Как нельзя говорить и о том, что один элемент находится после другого. Мы можем лишь сказать, принадлежит ли этот элемент данному множеству или нет. Отсюда также следует, что один и тот же элемент не может встречаться более одного раза в любом множестве.

Для характеристики объема множества вводят понятие его размера, т. е. количество содержащихся в нем элементов. Существуют пустые множества, не содержащие не одного элемента. Но более интересен случай, когда множество является бесконечным. Для характеристики подобных множеств, содержащих неограниченное число элементов, введено понятие мощности множества, которое является расширенным определением размера для конечных множеств. Естественно, что мощность в этом случае уже не может быть выражено каким-либо конкретным числом. Оно лишь указывает на соотношение (меньше, больше или равно) данного множества с некоторыми эталонными, для каждого из которых вводится специальная характеристика — кардинальное число. Так множество всех натуральных чисел (1, 2, 3… и так далее до бесконечности) принято называть счетным множеством, а его кардинальное число обозначать первой буквой древнееврейского алфавита алеф с индексом «нуль» (алеф-нуль). Любое (бесконечное) множество, сравнимое со счетным, имеет такую же мощность.

Чтобы сравнивать бесконечные множества необходимо построить взаимно однозначное соответствие между ними (или показать, что такое соответствие невозможно). Это означает, что каждому элементу из одного множества следует постараться поставить в соответствие единственный элемент из другого и наоборот. При этом мы не обязаны строить такое соответствие «вручную». Достаточно указать правило, по которому оно возможно.

Немецкий математик Георг Кантор подобным образом показал, что множество всех целых, и даже множество всех рациональных (дробных) чисел имеет мощность алеф-нуль. То есть такие множества соизмеримы с множеством всех натуральных чисел. И хотя они все бесконечные, они содержат как бы «одинаковое» (бесконечное) число элементов. Или, если так можно выразиться, одинаково бесконечны.

На самом деле показать такое соответствие не так уж и сложно.

Так представим множество всех целых чисел

…, -n,…, -3, -2, -1, 0, 1, 2, 3, …, n, …

в виде таблицы из двух бесконечных строк, записав отрицательные элементы под положительными:

0, 1, 2, 3, …, n, …

-1, -2, -3, …, -n, …

Теперь, начав последовательно двигаться по ее элементам как показано ниже (Рисунок 12), мы сможем в пределе занумеровать каждый из них. То есть указать (причем, достаточно просто) взаимно однозначное соответствие между этим множеством и множеством натуральных чисел (штриховые линии на рисунке).

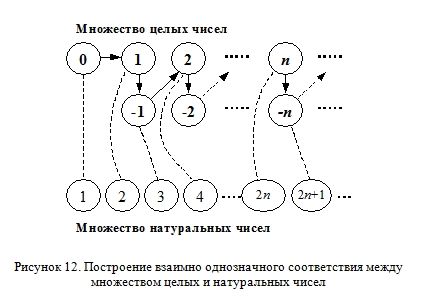
Математически это означает, что сумма двух счетных множеств счетно.

Для рациональных чисел такое соответствие построить сложнее, но не на много. Действительно, так как любое рациональное число r может быть представлено в виде несократимой дроби, то представим множество всех рациональных чисел в виде бесконечной таблицы (Рисунок 13).

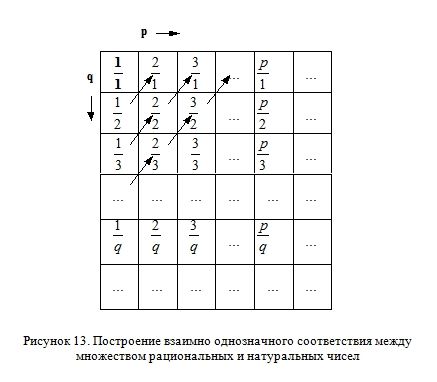
Для простоты изложения ограничимся лишь положительными числами r=p/q, где p и q — натуральные. Начав нумеровать ее элементы с верхнего левого угла по диагоналям (переходя последовательно, скажем, с первого столбца по первую строку), мы также сможем в пределе их все занумеровать.

Математически это означает, что произведение мощностей двух счетных множеств есть мощность алеф-нуль.

Более того, множество всех рациональных точек n-мерного пространства и множество всех алгебраических чисел также оказывается счетным. Такие множества, будучи бесконечными, дискретны по своей структуре (как и множество натуральных чисел). То есть всегда имеется возможность, перенумеровав их элементы, перейти от одного к другому, указав для него соседний элемент. Или, что то же самое, между двумя соседними элементами нет никаких других элементов. Неважно, что структура представляемого таким образом множества может быть многомерной. Главное, что она конечномерная.

Возникает резонный вопрос: «Все ли известные математике множества счетны?». Оказывается, что нет. Рассмотрим множество всех действительных чисел. Как бы мы не пытались занумеровать его элементы, всегда останется бесконечное множество «пропущенных». Причем это множество будет опять таки несчетным. Доказательство этого утверждения на самом деле несложно, однако, на мой взгляд, не слишком интересно, чтобы приводит его здесь. Интересующийся читатель может найти его в любом учебнике по теории множеств.

Действительное число представимо, в общем случае, как бесконечная непериодическая десятичная дробь. Например, известное число пи (отношение длины окружности к ее диаметру) π=3,1415926536…

Вообще говоря, и рациональные числа при десятичной форме записи образуют бесконечные дроби (за исключением целых чисел.).

Но такие дроби имеют период. То есть с какого-то определенного места последовательность цифр после запятой начнет строго повторяться. Поэтому для записи любого рационального числа (как в форме несократимой дроби, так и в форме бесконечной десятичной) нам потребуется ограниченное (конечное) число цифр. Действительное же число, будучи, как было сказано, непериодическим, требует для своего представления бесконечное множество цифр (от нуля до девяти). Понятно, что такое множество цифр будет иметь мощность алеф-нуль. Поэтому все наши ресурсы при попытке занумеровать множество действительных чисел уйдут на представление лишь какого-нибудь одного единственного числа!

Мне могут возразить, что вовсе не обязательно точно представлять каждое действительное число в отдельности. Достаточно указать правило, по которому эти числа смогут быть вычислены с требуемой точностью (а в пределе и с бесконечной). Так говоря о числе π, мы просто даем его определение, как способ вычисления: «отношение длины окружности к ее диаметру». Мы можем давать и более сложные алгоритмы нахождения чисел, составляющих определяемые таким образом новые множества. Но такие определения будут содержать в себе конечный набор условий принадлежности элемента к тому или иному набору.

Когда мы вводили множество всех целых чисел, мы добавляли к уже существующим положительным натуральным числам еще отрицательные (ну и еще число нуль). То есть множество алеф-нуль удвоилось, а к определению натуральных чисел добавился атрибут «знак числа».

Для представления любого рационального числа требуется уже два натуральных. Но мощность подобного множества опять не меняется.

В общем случае, пока для представления каждого элемента формируемого множества нам требуется конечное число натуральных чисел, получаемое таким образом множество будет счетным.

На самом деле проблема несчетности множества действительных чисел возникла вовсе не из-за трудности представления какого-то отдельного иррационального числа, а в том, что принципиально не возможно дать определение любому его элементу. А раз так, то мы просто вынуждены представлять каждый его элемент в подобной «грубой» форме, как бесконечная последовательность цифр, расходуя уже на один элемент все свои бесконечные ресурсы. Такая проблема не возникала для, скажем, таких иррациональностей, как корень квадратный из двух, хотя они так же не представимы в виде десятичной периодической дроби. Ведь для однозначного определения таких элементов нам потребуется всего лишь ограниченный набор рациональных чисел — коэффициентов многочлена, приравнивая нулю который, мы способны (пусть и теоретически) находить их.

Если бы мы смогли дать подобное правило для вычисления каждого действительного числа, то задача была бы решена, и мощность этого множество была бы алеф-нуль. Но мы не способны, мысля ограниченно, дать такое определение. Подобное множество находится выше наших представлений.

С точки зрения комбинаторики множество всех действительных чисел может быть определено, как множество всех подмножеств множества натуральных чисел. Его мощность называется мощностью континуума, от латинского continuum — непрерывный. Действительно, геометрическим аналогом множества действительных чисел служит совокупность всех точек на бесконечной прямой. А пространство, как известно, принято считать непрерывным.

Георгу Кантору потребовалось еще три года, чтобы показать, что и мощность любого конечного отрезка бесконечной прямой равна мощности всей этой прямой, а в квадрате содержится столько же точек, как в отрезке его стороны. Таким образом, всех натуральных чисел не хватит, чтобы занумеровать даже небольшой конечный отрезок всей действительной оси, скажем интервал [0, 1]. Это объясняется несоизмеримостью дискретных счетных множеств и непрерывных множеств мощности континуума.

К первым, как было показано, относится множество дискретных чисел на прямой (целые числа), множество дискретных чисел на плоскости (рациональные), множество дискретных чисел в n-мерном пространстве (алгебраические числа n-ого порядка).

Ко второму классу относятся такие непрерывные множества, как все точки на прямой, множество точек на плоскости и в любом пространстве.

Переход к бесконечно малым величинам заставил математиков говорить о непрерывных случайных величинах, состоящих из множества событий с нулевой вероятностью, а физиков — о материальной точке, не имеющей конечной массы.

Так в одном из учебников по теории вероятностей для ВУЗов находим следующее положение: «Вероятность любого отдельного значения непрерывной случайной величины равна нулю» ([2], с. 79).

Подобное утверждение следует из предположения о бесконечном множестве возможных значений непрерывной случайной величины. Понятно, что в этом случае конечное (дискретное) множество конкретных выбранных значений имеет меньшую мощность и эти множества просто несоизмеримы.

Чтобы объяснить подобное явление автор указанного учебника приводит такую аналогию из физики: «Понятие о событии “возможном, но обладающем нулевой вероятностью” кажется на первый взгляд парадоксальным. В действительности оно не более парадоксально, чем представление о теле, имеющем определенную массу, тогда как ни одна из точек внутри тела определенной конечной массой не обладает» ([2], с. 79).

Действительно, везде, где мы говорим о непрерывных (аналоговых) величинах мы должны мириться с подобными «эффектами». Так при непрерывном распределении вероятностей вероятность попадания на сколь угодно малый участок может быть отлична от нуля, тогда как вероятность попадания в строго определенную точку в точности равна нулю (а событие противоположное рассмотренному, наоборот имеет вероятность, равную единице, но не достоверно).

Именно в переходе от дискретного к непрерывному и заключается основное отличие в поведении счетного множества и континуума.

В счетных множествах каждому элементу можно найти соседний (соседние). В несчетных же множествах понятие соседний элемент лишено смысла, ибо какие бы две различные точки мы не взяли, между ними всегда будет заключено бесконечное число других точек (мощность этого множества равна с). Поэтому переход от одной фиксированной точки к другой возможен лишь в бесконечном пределе. Именно с этим связан парадокс Зенона со стрелой, рассмотренный нами в начале этой главы. То, что позволительно в абстрактной математике, не находит в данном случае реального примера в окружающей нас физической действительности. В отличие от математика, оперирующего с понятиями бесконечности, мы в реальной жизни имеем дело лишь с ограниченными категориями.

Впрочем, и с математической позиции с определением бесконечность не все так просто. Рассмотрим этот вопрос несколько более подробно.

Конечность или бесконечность

А самое главное, в гостинице было бесконечно много номеров.

Выгонты надеялись, что теперь никому больше не придется слышать

порядком надоевшую им за время скитаний фразу:

«Свободных номеров нет».

Н.Я. Виленкин. «Межзвездные скитания Йона Тихого»

Давным-давно, когда книги были деревьями… Люди уже умели считать, однако предел счета был ограничен. Трудно сказать, чем было вызвано ограничение числом шесть, но факт, что уже число семь воспринималось, скажем, еще у древних шумеров, как синоним слова много. Современные пословицы и поговорки, тому подтверждение («Семь раз отмерь, один раз отрежь», «Один с сошкой, семеро с ложкой», «Семеро одного не ждут» и т. д.).

Постепенно люди учились выражать все большие и большие числа. Переход к позиционной системе счисления позволил легко и компактно выражать огромные числа. Так еще Архимед в III веке до н. э. использовал оригинальный метод счисления, описанный им в сочинении «Исчисление песчинок», позволивший ему называть огромные числа.

Сейчас мы способны с необычайной легкостью не только пересчитать все нейтроны в нашей Метагалактике, но и придумать такие числа, что даже трудно будет представить их смысл.

Тем не менее, любое из этих чисел будет конечным, а в математике широко применяется понятие бесконечно больших величин или, просто, бесконечность. Для этого существует специальное обозначение (повернутая набок восьмерка). Существует так же плюс бесконечность и минус бесконечность. Определены и некоторые операции над ними, как скажем деление числа на бесконечность.

Подобные приемы вводят в искушение представлять бесконечность, как обычное вполне определенное число, говоря о ней, как о существующей реальности. Однако это является недопустимой ошибкой.

Бесконечность никогда не сможет быть выражена или определена не через какие числа, какими бы огромными они не были. Это понятие существует «вне чисел» и отражает факт нашего незнания о количественном описании. То есть оно является лишь качественной характеристикой. Как только мы попытаемся зафиксировать, определить бесконечность и точно выразить ее через конкретные численные обозначения, она перестанет ею быть. А раз так, то нельзя говорить о ней, как о объективно существующей реальности.

Математики понимают это и различные бесконечно большие (и бесконечно малые) величины определяют через понятие предел. Скажем, парабола x^2 неограниченно возрастает при аргументе x стремящемся к бесконечности. Но что означает «стремящимся к бесконечности»? Допустим мы задаем нулевое начальное значение аргумента (x=0), а затем беспрестанно увеличиваем его на единицу (x:=x+1). Этот процесс при этом должен длиться вечно, т. е. мы опять переходим к понятию бесконечности, но на этот раз времени. А так как мы не способны познать, что такое вечность, то и не можем «пощупать» бесконечное. Другими словами, бесконечность не может быть охарактеризована как статическая реальность, а лишь как динамический процесс самовоспроизводства.

«Король математиков» Карл Фридрих Гаусс писал: «Я протестую против употребления бесконечной величины, как чего-то завершенного, что в математике никогда недопустимо. Бесконечность не нужно понимать буквально, когда речь идет собственно о пределе, к которому сколь угодно близко приближаются определенные отношения, когда другие принимаются неограниченно возрастающими» (цит. по [4], с. 21).

В начале XX века среди ряда математиков, специалистов в теории множеств, разгорелся серьезный спор, вызванный, в первую очередь, так называемой континуум гипотезы (проблемой континуума). Ряд видных французских математиков (Адамар, Борель, Бэр, Лебег и Цермело) опубликовали свою переписку о том, что же такое бесконечность, и какие бесконечные множества следует считать существующими.

Лузин Н. Н., русский математик, один из основателей Московской математической школы, так описывал этот спор. «Если анализировать взгляды творцов современной теории функции, легко подметить, что каждый из них в процессе своей работы исходит из определенной концепции возможного и допустимого, за пределами которого кончается область математики и начинается область, лежащая, по выражению Бореля, вне математики… Если, следуя примеру Максвелла, приписать область возможного и исполнимого того или иного автора соответствующему воображаемому существу, то получится следующая схема» (цит. по [4], с. 21). И далее Николай Николаевич приводит следующую «иерархию демонов» (в порядке возрастания их «могущества»): «демон» Брауэра, «демон» Бэра, «демон» Бореля, «демон» Лебега и, наконец, «демон» Цермело. Если указать для каждого из них сферу их «влияния», а также область не подвластную их «способностям» (трансцендентная область, выражаясь терминами Канта), то получим следующую таблицу.

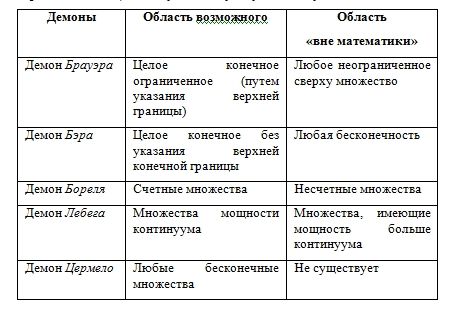
 Точка зрения самого Лузина по дискутируемым проблемам была не однозначной. Чаще всего он стоял на позиции Бореля (существование счетных множеств). К понятию же несчетной бесконечности относился как к «чисто отрицательному, не имеющему никакой объективной реальности» (цит. по [4], с. 142). Иногда же он склонялся даже к позиции Бэра, утверждая, что мы не имеем достаточно ясной концепции актуальной бесконечности. «Фундаментальная проблема состоит в том, чтобы выяснить, является ли последовательность целых положительных чисел вполне объективной. Кажется, что она почти объективна и что имеются следы несомненной субъективности, такой, что нельзя говорить о последовательности целых положительных чисел всегда, во всех случаях, в одном и том же смысле» (цит. по [4], с. 142).

Постараемся взглянуть на указанный квинтет «демонов от математики» с несколько другой позиции.

Какой аналог мы можем поставить демону Брауэра? На мой взгляд, лучшим примером может служить обычный современный цифровой компьютер. На самом деле, он, во-первых, состоит их ограниченного набора элементов, а, во-вторых, работа с этими элементами производится так же дискретным образом.

«Каждая программа для ЭВМ, будучи воплощением некоторого алгоритма, представляет собой конструктивный объект. Это свойство конструктивности проявляется двояко: с одной стороны, программа строится посредством определенного конечного множества операцией, а с другой, все объекты, которыми она манипулирует, также создаются посредством некоторого конечного множества операций. Программа может иметь дело с любым множеством объектов, даже с потенциально бесконечным, но в любой данный момент времени это множество конечно» ([7], с. 7).

Скорее всего, мы, воспринимая окружающий нас Мир, так же имеем дело в определенное мгновение (квант времени) с ограниченным набором категорий. Такой вывод напрашивается исходя хотя бы из того, что количество нейронов, нервных окончаний и любых клеток в нашем организме ограничено.

Норберт Винер, описывая ограниченность человеческого логического мышления, отмечает (курсив его): «Всякая логика, имеющая для нас смысл, не может содержать ничего такого, чего человеческий разум, а следовательно и человеческая нервная система не были бы способны объять. Всяка логика ограничена в силу ограничений человеческого ума, которым он подвержен в деятельности, именуемой логическим мышлением» ([5], с. 193).

Таким образом, наше поведение, как и работа полностью детерминированного цифрового компьютера попадает под «юрисдикцию» демона Брауэра, имеющего дело с целыми (дискретными) конечными, причем ограниченными (в каждый момент времени) множествами. Только в отличие от устройства ЭВМ, в реальной жизни мы не способны явно указать строгие границы нашего Мироздания. Это вовсе не должно означать, что мы имеем дело с бесконечной субстанцией. Просто пытаясь найти подобные границы окружающего нас Мегамира или предел элементарных частиц в микромире, мы будем постоянно наталкиваться на различные логические преграды. Поиски «края Земли» всегда будут заканчиваться неудачей. Этот «край» незаметно, но с видным постоянством будет ускользать от нас каждый раз, когда мы, казалось вот-вот приблизились к нему на достаточно близкое расстояние. Действительно, любые попытки добраться до горизонта всегда оказываются тщетными.

Sub specie aeternitatis[2]

Пожалуй, еще Аристотель различал понятия актуальной и потенциальной бесконечности. Иначе говоря, существующей и становящейся. Как человеку, знакомому с теорией и практикой программирования не понаслышке, такое разделение мне представляется особенно интересно в разрезе теории алгоритмов.

 «Метаморфозы, происходящие с трактовкой типа данных, до некоторой степени являются отражением кризиса, начавшегося в математике на рубеже XX века и продолжающегося до сих пор. Как известно, в то время в теории множеств был обнаружен ряд противоречий (парадокс Кантора, парадокс Рассела и др.). Эти парадоксы в значительной мере обусловлены тем, что в теории множеств допускаются “готовые”, завершенные бесконечные множества, называемые актуальными бесконечными множествами» ([7], с. 6).

Криницкий Н. А. в книге «Алгоритмы вокруг нас» пишет о таких актуальных бесконечностях: «Расходуя ограниченное количество ресурсов на каждом шаге, имеющем фиксированную длительность, построить такое множество ни реально, ни потенциально нельзя. Проверить, обладают ли все элементы такого множества каким-либо свойством, тоже нельзя, так как никакая ограниченная скорость проверки не дает возможности охватить их все. Другое дело, потенциально бесконечное, или потенциально осуществимое множество. Такое множество, в каждый момент конечно, но есть прием, позволяющий добавить к нему всегда еще несколько (а значит, сколько угодно) элементов. Анализ элементов такого множества можно провести исследованием правила, которое позволяет получать все новые и новые элементы этого “конструктивного” множества» (цит. по [7], с. 6-7).

Я отношу наше с вами Мировосприятие к компетенции именно демона Брауэра (а не Бэра), так как, несмотря на кажущуюся перспективу охватить нашим сознанием любое (пусть и не бесконечное) множество, осуществить это на самом деле невозможно. До тех пор, пока физики не заглянули в «темные закоулки» микромира, в умах большинства ученых царила эйфория полной уверенности добраться до «самых-самых» элементарных частиц – кирпичиков нашего Мироздания. Тот же Аристотель различал виды бесконечностей, называемых сейчас экстенсивной и интенсивной. Первая из них возникает при последовательном и безграничном добавлении новых предметов, а вторая при безграничном углублении в строение изучаемого объекта. Однако опыты с изучением микрообъектов на квантовом уровне показало несостоятельность возможности бесконечно двигаться «внутрь» материи. Подобная ситуация существует, по всей видимости, и с Мегамиром. Поиск четкой границы Вселенной навряд ли сможет увенчаться успехом, даже отбросив в сторону наши технические ограничения. Подобные трудности возникают, в первую очередь, в логическом плане.

Мы не способны уподобиться демону Бэра и рассматривать любые множества без указания верхней границы. Такая граница в нашем Мировосприятии безусловно существует. Обусловлена она, по всей видимости, некой физической ограниченностью и носит фундаментальный характер. То есть перешагнуть ее, улучшая лишь инструментальные средства, мы не сможем.

Именно этим в первую очередь современная физика отличается от «классической» физики времен Ньютона. Пожалуй, наиболее значимым событием смены парадигм в описании физической картины Мира стало введение в начале XX века специальных фундаментальных констант в уравнения, описывающие характеристики пространства и времени. Так в теории относительности было показано, что скорость света (скорость распространения электромагнитных волн в вакууме) является в нашей Вселенной максимально возможной и не зависит от выбранной системы отсчета. Причем ее абсолютная величина (с=3·10^8 [м/с]) оказалась весьма скромной по меркам космических расстояний Мегамира. В квантовой механике такой константой стала постоянная Планка, накладывающая фундаментальные ограничения на возможность изучения объектов микромира при помощи «классических» методов.

Английский физик-теоретик Дирак считал, что «существует предел тонкости наших средств наблюдения и малости сопровождающего возмущения – предел, который присущ природе вещей и никогда не может быть превзойден совершенствованием техники или искусства экспериментатора» (цит. по: [10], с. 51).

При таком положении дел вопрос о бесконечности микро- и Мегамира становится бессмысленным. Существование даже просто очень маленьких, и очень больших конечных величин в воспринимаемом нами окружающем физическом Мире и то ставится под сомнение. Говорить, скажем, о частице размером менее 10^-100 метров (по крайней мере, в том смысле какой мы вкладываем смысл в понятие «частица») уже неправомочно. Так же вряд ли имеет смысл и вопрос о том, что распложено на таком громадном расстоянии в как 10^100 световых лет от нас.

В русском переводе второго издания (1986 г.) английского словаря “Dictionary of Computig” издательства “Oxford University Press” [13], мы находим следующее замечание относительно определения дискретных и аналоговых систем (выделение моё) (“D.223. discrete and continuos systems”):

• Вопрос о принадлежности сигнала (или его источника) к чисто дискретному или чисто аналоговому классу неразрешим, поскольку для постановки соответствующего эксперимента потребуется бесконечно широкая полоса частот (bandwidth) (или бесконечное время), а также бесконечное отношение сигнал/шум (signal-to-noiseratio), которых невозможно достичь в практических условиях.

Здесь под определением практические условия в контексте этой главы можно подразумевать ограниченное пространство демона Брауэра, который не способен делать «метафизические» заключения о категории непрерывного.

Высказывание Козьмы Пруткова: «Нет столь великой вещи, которую не превзошла бы величиною еще большая. Нет вещи столь малой, в которую не вместилась бы еще меньшая», справедливо больше для жизни демона Бэра, чем для нашей с вами.

Я не утверждаю, что Ленин заблуждался, когда говорил о неисчерпаемости атома и электрона. И спустя сто лет не была найдена «самая-самая» элементарная частица строения нашего мироздания. Однако, и наивное представление электрона, как «матрешки», внутри которой наложены другие вместилища для частичек, – также неверно. Электрон, быть может, действительно неисчерпаем, но не в «механическом» понимание этого слова. Просто его исчерпание способно происходить и на другом уровне. (Скажем всем известно, что бит – минимальная единица информации. Действительно, он способен принимать только два значения (например, ноль или единица). Но это не означает, что он неделим. Допустим, мы как-то разделили его на две эти составляющие (0 и 1). Бит перестал существовать как единица информации, но превратился в две константы.)

То, что можно создать в «чистой» математике не всегда можно найти в воспринимаемой нами физической реальности. Это не должно означать, что реальный «настоящий» Мир обладает тотальным свойством дискретности и ограниченности. Напротив, мне представляется, что как раз противоречия, возникающие при наших попытках «пробиться» на квантовый уровень микрочастиц, вызваны существованием других интерпретаций Мироустройства.

Как было сказано, вслед за демоном Брауэра шествует его более «могучий» коллега – демон Бэра. Рано или поздно он сможет проанализировать множество любого, но конечного объема. При этом он не будет натыкаться на различные преграды. Иными словами, он имеет дело с потенциальными бесконечностями.

Далее, «над ним» находятся еще более могущественные демоны Бореля и Лебега. Они способны работать уже с актуальными бесконечностями.

Первый может охватить все множество натуральных чисел, т. е. начав с первого элемента, способен последовательно шаг за шагом просмотреть всю бесконечность, а не просто наперед заданную область. Другими словами у этого демона нет ограничений во времени. На Востоке в глубокой древности была сложена притча: «Вот алмазная гора высотой в тысячу локтей. Раз в столетие прилетает птичка и точит свой клюв о гору. Когда она сточит всю гору, пройдет первой мгновение вечности» (цит. по [4], с. 7-8). Так вот, демон Бореля живет в таком «вечном» времени, сильно отличающемся от нашего. Чтобы продемонстрировать его возможности приведу следующий пример. В 1907 году Брауэр, опираясь на мнения, неоднократно высказывающиеся Кронекером и Пуанкаре, предпринял попытку ввести новый метод работы с бесконечными множествами. Это направление получило название интуицизма. Оно отвергало «чистые доказательства существования» и требовало каждый раз предъявления конкретного примера объекта, обладающего данным свойством. Иными словами, в качестве доказательства чего-либо интуиционисты принимали лишь описание конструкции соответствующего объекта. (Кроме того, они категорически отвергали один из основных законов аристотелевой логики, так называемый закон исключения третьего. Его суть состоит в том, что любое высказывание является либо истинным, либо ложным – Tertium non datur – третьего не дано).

В одном из докладов об интуиционизме Брауэр привел в качестве примера утверждение, которое тогда нельзя было ни доказать, ни опровергнуть, следующее: «В десятичном разложении числа π идут десять цифр подряд». Действительно, в те времена было известно лишь чуть более семисот десятичных знаков для этого трансцендентного числа, да и то большая часть из них оказалась неверной. Сейчас с помощью ЭВМ вполне возможно доказать приведенное утверждение. Но если заменить число 10 скажем на 10^1000, то можно быть уверенным, что наша задача вычисления необходимого для проверки этой гипотезы количества десятичных знаков окажется неразрешимой для любых машин, которые когда-либо смогут быть построены. А так как теоретически решить проблему тоже невозможно, то утверждение о наличии в десятичном разложении числа π 10^1000 идущих подряд девяток заведомо непроверяемо. Правда, один из математиков, присутствующих на докладе Брауэра, сказал, что хотя мы и не знаем, верно это утверждение или нет, но господь-бог знает. «Я не имею прямой связи с богом», – сухо возразил Брауэр ([4], с. 150).

В данном случае в роли такого «господа-бога» мог бы выступить упомянутый демон Бореля. Число π, будучи трансцендентным, представимо в виде бесконечной непериодической десятичной дроби, т. е. содержит в своем разложении все мыслимые и немыслимые комбинации цифр. Поэтому демон Бореля способен не только подтвердить наличие в десятичном разложении π 10¹⁰⁰⁰ идущих подряд девяток, но найти любую другую еще более сложную последовательность (причем бесконечное число раз!)[3]

 Однако и такой «монстр» способен «жить» только в дискретной среде. Всей его вечности не хватит, чтобы проанализировать даже маленький участок непрерывного пространства. Такая задача уже «по зубам» демону Лебега. Не только вечность во времени, но и бесконечность в пространстве для него обычное дело, ибо областью возможного для него являются множества с мощностью континуума.

Грубо говоря, подобные бесконечные множества для этих демонов (Бореля и Лебега) бесконечными (в нашем понимании этого слова) и не являются. Дело в том, что для них это уже просто статические (законченные) сущности.

Но самым удивительным демоном является, безусловно, демон Цермело. Для него нет вообще никаких преград, и любые бесконечные множества ему по силам.

Если в случае предыдущих двух демонов нам было трудно найти им подходящий физический пример, то этому «чудищу» невозможно подыскать и пример математический. Ведь как было сказано ранее, не существует множества самой большой мощности (множества всех множеств)!

Если изобразить рассмотренную иерархию «математических демонов», то получится вот такая схема (Рисунок 14).

Каждый из демонов (кроме демона Цермело) отделен от последующего непроницаемой стенкой (сплошные линии на рисунке). За ней находится трансцендентная (словами Канта) область. Только демон Цермело лишен такого ограничения.

Мы с вами попадаем в первую область – область действия демона Брауэра, имеющего дело с ограниченными и дискретными множествами. Внутри нее расположены объекты, которые хотя и существенно отличаются друг от друга, но лишь в количественном плане. К примеру, современный компьютер находится здесь же, но чуть ниже нас.

Качественный же скачок возможен лишь при переходе через границу «трансцендентности» в область более могущественного демона.

О нечто похожем говорит и Франклин Меррелл-Вольф, когда объясняет раздвоение двойственного сознания человека тем, что оно обладает только двумя функциями, органами или способностями познания, а именно чувственным восприятием и умозрительным постижением ([14], с. 11). В качестве иллюстрации он приводит следующую схему (Рисунок 15). 

 Он описывает ее так: «Ниже прямой простирается область двойственного сознания, а выше – область недвойственности, куда разум не способен проникнуть без помощи со стороны. Я утверждаю, что разум в состоянии самостоятельно превзойти любую ранее достигнутую высоту и что в дальнейшем он никогда не достигнет уровня, который не смог бы затем перерасти. Но выше этой линии ему все же не подняться» ([14], с. 12). И далее: «разум не в состоянии подняться выше начерченной линии, хотя может превзойти любой уровень, которого уже достиг или достигнет в будущем. Это означает, что, имея в своем распоряжении конечное время, вы всегда способны совершить еще одну операцию сложения. Иными словами, разум может возвыситься до такой степени, что его удаленность от этой прямой окажется меньше любого предопределенного расстояния, каким бы малым оно ни было. Можно возразить, что такие подъемы будут несущественными, так как изменения расстояний слишком малы, но это не совсем так. Подобные свершения могут оказаться очень значительными – я здесь не ставлю никаких ограничений. Таким образом, без посторонней помощи разум может вечно двигаться ввысь – но он никогда не пересечет этой прямой. То есть навсегда останется в области двойственного сознания» ([14], с. 14).

Франклин Меррелл-Вольф отмечает: «наши рассуждения о наблюдаемой вселенной достоверны только в пределах двойственного сознания. В этом-то и вся сложность. Вы можете сказать: “Я не могу представить себе иное сознание, нечто другое”. Да, совершенно верно. Разве ограниченное, двойственное сознание способно вообразить отсутствие двойственности?». И здесь же: «Не стоит даже пытаться определять ТО, что находится за любыми границами. Определения применимы только в мире двойственного сознания, но наши концепции не пригодны для ТОГО, что кроется за любыми пределами, и только при искусном обращении они могут дать легкий намек на ТО» (([14], с. 29).

Как писал Гёте в «Фаусте»:

• Но у природы крепкие
  То что она желает скрыть в тени таинственного своего покрова,
  Не выманить винтами шестерни, ни силами орудья никакого[4].

«Классическая» схема аналогово-цифрового преобразования

Под сладкими выражениями таятся мысли коварные:

так, от курящего табак нередко пахнет духами.

Козьма Прутков. «Мысли и афоризмы», №5

Исходя из вышесказанного, следует признать, что широко используемое определение «аналоговое» как описание бесконечного и непрерывного, неприменимо в нашем понимании. Так наше дискретное восприятие не позволяет нам с полным объективным правом говорить о переводе аналогового сигнала в цифровой и наоборот. И в том, и в другом случае мы должны понимать, что происходит лишь масштабирование точности дискретного сигнала, то есть его огрубление или сглаживание.

При таком положении дел, об «истинно» аналоговом сигнале мы не можем сказать что-либо определенное, ибо это есть суть понятия выше нашего уровня сознания. Поэтому «классическая» схема аналогово-цифрового преобразования мне представляется несколько ошибочной. Напомним ее основные этапы.

Эта последовательность перевода аналога в цифру подразумевает преобразование непрерывного (бесконечно точного) сигнала в ограниченный сигнал, допускающий представление в дискретной форме. Здесь под термином сигнал мы просто подразумеваем какой-либо параметр, изменяющийся во времени.

Аналогово-цифровое преобразование заключается в выполнении трех основных операций: дискретизации, квантования и кодирования (Рисунок 16). Дискретизация (sampling) – представление непрерывного сигнала (analogsignal) последовательностью его значений (отсчетов). Эти отсчеты берутся в моменты времени, отделенные друг от друга интервалом дискретизации (T). Величину, обратную интервалу между отсчетами, называют частотой дискретизации.

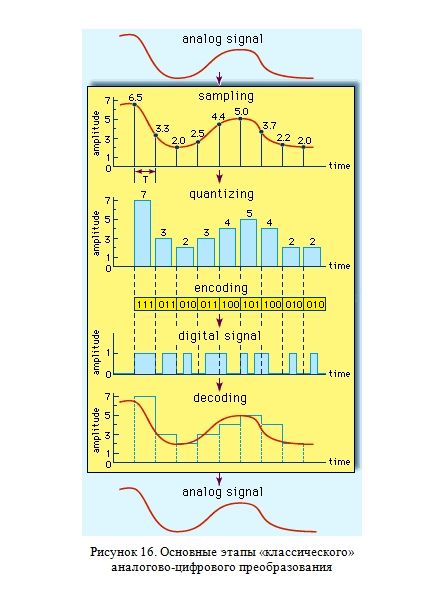
Квантование (quantizing) представляет собой замену величины отсчета сигнала ближайшим значением из набора фиксированных величин – уровней квантования. Другими словами, квантование – это округление величины отсчета (вынужденное огрубление по уровню сигнала). Уровни квантования делят весь диапазон возможного изменения значений сигнала (amplitude) на конечное число интервалов – шагов квантования. Расположение уровней квантования обусловлено шкалой квантования.

Цифровое кодирование (encoding) является завершающим этапом аналогово-цифрового преобразования. Квантованный сигнал в отличие от исходного аналогового может принимать только конечное число значений. Это позволяет представить его в пределах каждого интервала дискретизации числом, равным порядковому номеру уровня квантования. В свою очередь, это число можно выразить комбинацией некоторых знаков или символов. Совокупность знаков (символов) и система правил, при помощи которых данные представляются в виде набора символов, называют кодом. Конечная последовательность кодовых символов называется кодовым словом. Квантовый сигнал можно преобразовать в последовательность кодовых слов. Эта операция и называется кодированием. Каждое кодовое слово передается в пределах одного интервала дискретизации.

Естественно, что от частоты дискретизации и числа уровней квантования напрямую зависит качество (и степень огрубления) получаемого цифрового сигнала.

Из цифры в цифру

Кто роется в заблуждениях – находит истину.

Геннадий Матюшов. «Афоризмы» №78

В противовес вышерассмотренной схеме представлю свою модель аналогово-цифрового преобразования. По моему мнению «истинно» аналоговые сигналы можно наблюдать только в «запредельных» для нашего уровня областях. Скажем в области демона Лебега. Мы не способны «напрямую» работать с ними, поэтому перед тем, как попасть к нам (в «родную» область демона Брауэра) непрерывный сигнал уже проходит через своеобразный глобальный АЦП и преобразовывается в дискретный сигнал с определенной частотой дискретизации и шкалой квантования. В силу того, что для человеческого восприятия такая частота весьма велика, а шкала квантования очень точная, мы просто не замечаем подобную прерывность и продолжаем считать сигнал непрерывным. И лишь на квантовом уровне при изучении явлений микромира, мы начинаем сталкиваться с подобными ограничениями.

Здесь схематично показана цепочка аналогово-цифровых преобразований начиная с области демона Лебега (Рисунок 17).

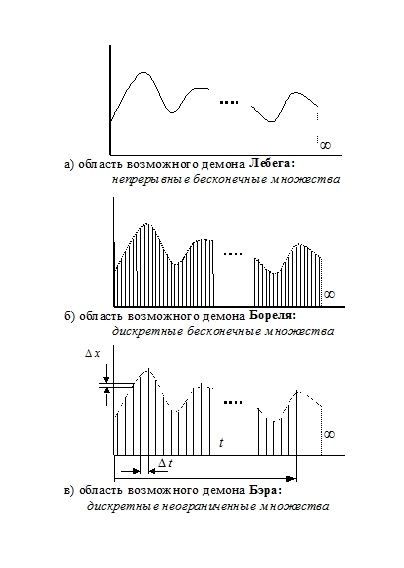
На рисунке «а» мы имеем «исходный» непрерывный сигнал причем бесконечный во времени (множество мощности континуума).

При переходе в область демона Бореля (рисунок «б») сигнал по прежнему остается бесконечным во времени, но его аналоговое представление заменяется счетной серий отсчетов (счетное множество). Значение каждого из них в точности равно величине исходного сигнала. Степень «густоты» таких отсчетов может быть выбрана какой угодно частой, но получить первоначальный сигнал невозможно.

Далее мы попадаем в область хотя и неограниченных множеств, но не являющихся актуально бесконечными (рисунок «в»). Мы можем охватить любой промежуток времени от 0 до t, однако значение параметра t все же конечно. Иными словами, демон Бэра формирует потенциальную бесконечность, и неограниченно большой параметр t не суть синоним слова бесконечность. При наличии достаточного запаса времени расстояние между отсчетами (∆t) может быть сделано сколь угодно малым, как и погрешность квантования (∆x). Однако абсолютно точное воспроизведение сигнала возможно лишь в переделе, т. е. никогда.

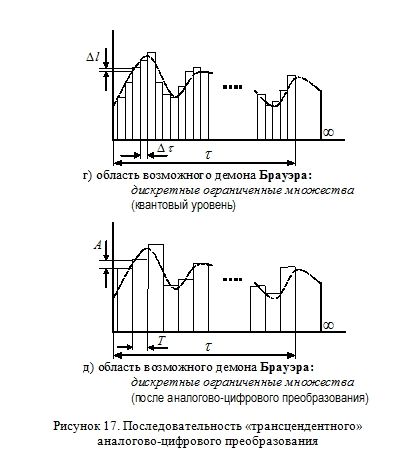
И, наконец, сигнал попадает непосредственно для нашего восприятия в область демона Брауэра (рисунок «г»). Видно, что сигнал уже квантован как по времени, так и по уровню. Причем в отличие от предыдущей области период дискретизации (∆τ) и уровень квантования (∆l) здесь не могут быть уменьшены ниже некоторого уровня. Ограничение в охвате во времени (τ) также носит, скорее всего, фундаментальный характер. Именно такой сигнал и принято называть аналоговым в нашем понимании этого слова.

Дальнейшая работа с таким сигналом подразумевает, например, уже описанное в предыдущем параграфе «классическое» аналогово-цифрового преобразование (рисунок «д»).