Три вида неправды

Известно шуточное высказывание Марка Твена о том, что существуют три вида неправды: обычная ложь, наглая ложь и статистика.

На примере строго математической задачи я постараюсь показать, насколько эта фраза соответствует действительности. Обойдемся без формул — будем разглядывать картинки и размышлять. Это совсем несложно.

Предположим, что одна фармакологическая фирма разработала некий препарат (назовем его «Препарат A»), способный помочь при определенном заболевании. Другая фирма (конкурирующая с первой) разработала аналогичный препарат (назовем его «Препарат B»).

Оба препарата сопоставимы по цене, прошли все необходимые испытания на безопасность и готовы к массовому производству.

Осталось изучить их эффективность, то есть выявить процент больных, которым лекарство поможет излечиться. С целью беспристрастности проверки фирмы передают свои препараты в клинику, где на излечении находятся больные именно этим заболеванием.

Главный врач клиники принимается лечить половину своих больных (для ровного счета пусть это будет 100 человек) Препаратом А, а другую половину (тоже 100 человек) — Препаратом B. (Для условий задачи можно было взять и другое количество пациентов — на вывод это никак не повлияет.)

Для удобства расчетов одну половину он помещает на первый этаж клиники, а другую — на второй, как схематично показано на Рисунке 1.

Мы исключаем влияние случайных факторов и считаем, что состав больных совершенно однороден, а врачом полностью соблюдены все требования по независимости эксперимента (например исключен эффект плацебо и подобные штучки, о которых прекрасно осведомлены серьезные исследователи).

Итак, больные на первом этаже надлежащим образом получают Препарат А, а на втором — Препарат B.

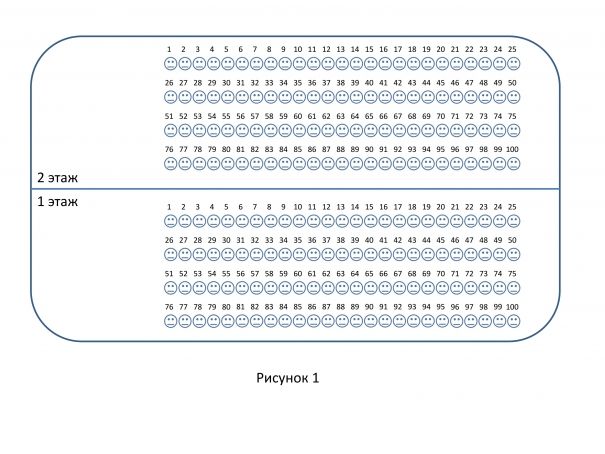
Для наглядности изобразим рожицы больных на первом этаже наклоненными налево, а на втором — направо (Рисунок 2).

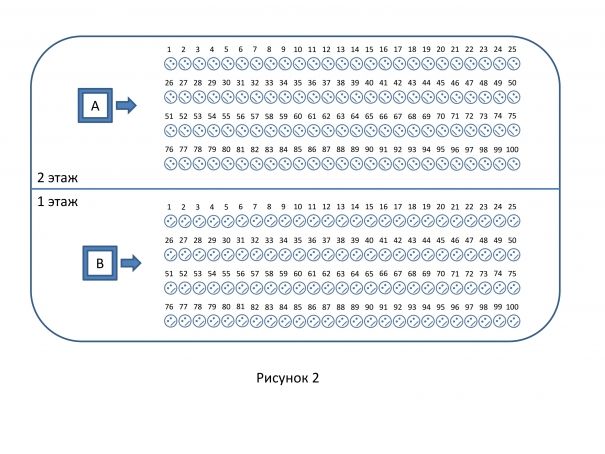
После проведенного курса лечения становится ясно, что эффективность Препарата А составила всего 20% (лекарство помогло 20 больным из 100), а эффективность Препарата B — аж 90% (излечилось 90 из 100). Отрыв больше, чем в 4 раза.

На Рисунке 3 красным цветом показаны улыбающиеся рожицы больных, для которых лечение оказалось эффективным, а серым цветом — грустные физиономии бедняг, которым препараты, увы, не помогли.

Очевидно, что эффективность Препарата B гораздо выше эффективности Препарата A. Очевидно? Очевидно!

Не сомневаясь в профессионализме и безупречной репутации главного врача, мы ожидаем, что его заключение отметит, что фирма, изготовившая Препарат B, однозначно обошла своего конкурента.

Но есть одна незадача… Фирма, изготовившая менее эффективный Препарат A, запланировала (совершенно безвозмездно!) в ближайшее время поставить в клинику столь необходимое современное медицинское оборудование. Понятно, что главному врачу как-то неловко давать настолько отрицательное заключение о Препарате A…

И вот тут начинается самое интересное.

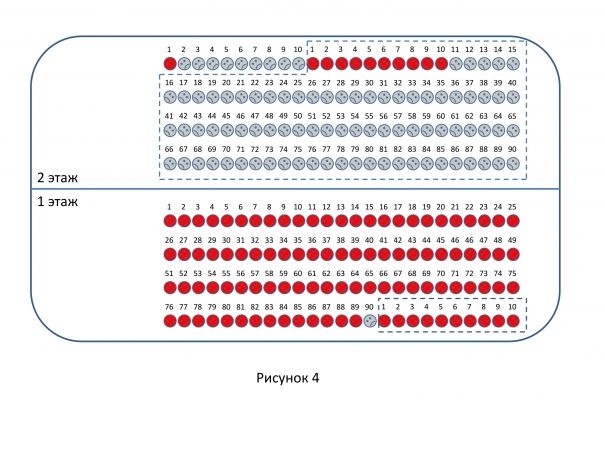
Наш замечательный главный врач на подлог и искажение данных исследования, конечно, не способен, но он решает просто переместить десять больных с первого этажа на второй, а десять больных со второго — на первый.

Нет же ничего криминального, если несколько человек поменяются местами?

Со второго этажа на первый он отправляет 10 счастливчиков, которым Препарат A помог, а с первого на второй переводит 9 бедолаг, которым Препарат B, к сожалению, помочь не смог и одного выздоровевшего (Рисунок 4).

От перестановки слагаемых сумма не меняется. Так ведь?

Нет не так.

По крайней мере, в статистике это не совсем так, и мы сейчас в этом убедимся.

Смотрим, что у нас получается с эффективностью препаратов. (Напомню, что красные улыбающиеся рожицы — это пациенты, которые выздоровели, серые грустные — которым препараты не помогли; если смайл повернут вправо — больной лечился Препаратом A, если влево — Препаратом B.)

На первом этаже из 90 больных, принимавших Препарат B, излечилось 89 (всего одна серая рожица на Рисунке 4). Что ж, эффективность очень высокая — больше 98%, почти 100%! Почти сто, но не сто. А эффективность бывшего аутсайдера — препарата A — оказывается именно 100%! На Рисунке 4 это десять счастливых рожиц, обведенных пунктирной линией. Десять из десяти! Ни одного неизлечившегося! Вот это да — Препарат A не только обошел конкурента, его эффективность вообще находится вне конкуренции!

Но позвольте, справедливо заметите вы — главврач просто отправил самых результативных в выздоровлении пациентов вниз, оставив наверху кучу недолеченных. Можно предположить, что статистика по второму этажу покажет низкую эффективность Препарата A, и таким образом расставит все точки в этом споре.

Разберемся!

Итак, что мы имеем по второму этажу клиники.

Препарат A, действительно, показывает низкую эффективность — всего 10 выздоровевших из 90 человек, обведенных пунктирной линией на Рисунке 4 (чуть больше 11 процентов). Однако, поразительно, что эффективность предыдущего лидера Препарата B еще меньше! Посмотрите еще раз на Рисунок 4 — из 10 больных, принимавших этот препарат, выздороветь удалось только одному (он под номером 1). Десять процентов эффективности Препарата B против одиннадцати Препарата A.

Поразительно, но это так.

Теперь главный врач со спокойной совестью может записать в итоговом отчете, что по результатам исследований Препарат A показал более высокую эффективность по сравнению с препаратом B в каждой из двух групп.

Ура, клиника теперь точно получит обещанное медицинское оборудование!

Хоть и с микроскопическим отрывом, но явный аутсайдер честно победил своего конкурента.

Но честно ли?

Нет, не честно.

Врач не имел право вмешиваться в распределение больных по этажам клиники после проведенного исследования. Умышленно перегруппировав излечившихся и неизлечившихся пациентов, он грубо исказил результат эксперимента и повлиял на его окончательный вывод. Несмотря на отсутствие ошибок в математических расчетах, сама методика научно неприемлема.

Однако кто из простых обывателей (в том числе потребителей подобных препаратов) способен заметить этот изъян? Конечно, надлежащий контроль наверняка выявит подобные случаи и отклонит скомпрометированные выводы. Но ведь можно использовать более изощренные способы искажения.

И вот что удивительно — незначительная на первый взгляд манипуляция (перемещение всего одной десятой части испытуемых) смогла кардинально повлиять на итог сравнения сразу по всем группам. И это при столь преобладающем отрыве победителя! (Напомню, что первоначально эффективность Препарата B превышала эффективность Препарата А в четыре с половиной раза!)

Статистика, как и теория вероятностей, относится к научным областям знания, которые интуитивно ну никак не воспринимаются человеческой психикой. Сюда же можно отнести теорию бесконечных множеств, различные интерпретации квантовой физики, постулаты теорий относительности Эйнштейна и, безусловно, теорию эволюции Дарвина. Выводы из этих теорий идут ну прямо таки вразрез со здравым смыслом. Впрочем, как метко заметил А. Эйнштейн, здравый смысл подсказывает нам, что Земля — плоская.

Все сказанное, надеюсь, убедит вас, насколько критически следует относиться к разнообразным, якобы, научным выводам.

Математика не лжет, но дьявол, как известно, прячется в деталях. Даже без явного подлога малейший изъян в условиях расчета способен полностью перечеркнуть истинность вывода.

Будьте внимательны и думайте своей головой!

Удачи!